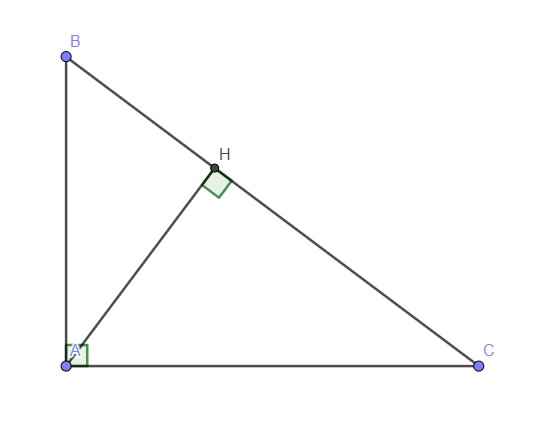
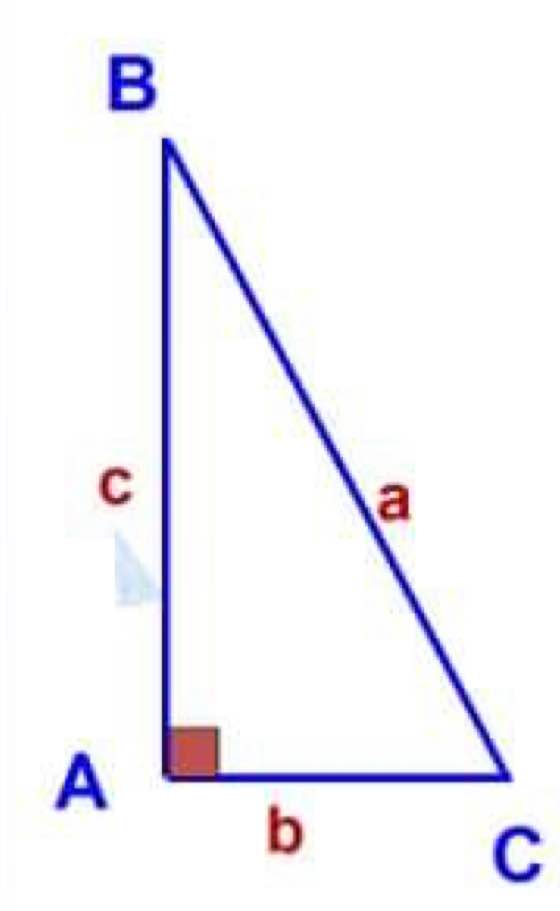
\(tanB=\sqrt{2}\Rightarrow\dfrac{AC}{AB}=\sqrt{2}\Rightarrow\dfrac{AC^2}{AB^2}=2\)
\(\Rightarrow\dfrac{AC^2}{AB^2}+1=3\Rightarrow\dfrac{AC^2+AB^2}{AB^2}=3\Rightarrow\dfrac{BC^2}{AB^2}=3\)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{1}{\sqrt{3}}\)
Mà \(sinC=\dfrac{AB}{BC}\Rightarrow sinC=\dfrac{1}{\sqrt{3}}\)
\(sin^2C+cos^2C=1\Rightarrow\dfrac{1}{3}+cos^2C=1\Rightarrow cosC=\dfrac{\sqrt{6}}{3}\)
\(tanC=\dfrac{sinC}{cosC}=\dfrac{\sqrt{2}}{2}\)
b.
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AC=\dfrac{AH}{sinC}=\dfrac{2\sqrt{3}}{\dfrac{1}{\sqrt{3}}}=6\left(cm\right)\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AB=\dfrac{AC}{tanB}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)
Áp dụng Pitago:
\(BC=\sqrt{AB^2+AC^2}=3\sqrt{6}\left(cm\right)\)
a: Xét ΔABC vuông tại A có
\(\tan\widehat{B}=\sqrt{2}\)
\(\Leftrightarrow AC=AB\cdot\sqrt{2}\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3\cdot AB^2\)
hay \(BC=AB\cdot\sqrt{3}\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
\(\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}\)
\(\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\cot\widehat{C}=\sqrt{2}\)