Question

Cho tam giác ABC nối tiếp (O;R).Tính độ dài các cạnh AB,AC,biết R = 3cm và khoảng cách từ O đến AB,AC lần lượt là 2√2 và √11/2 cm

Answer 1

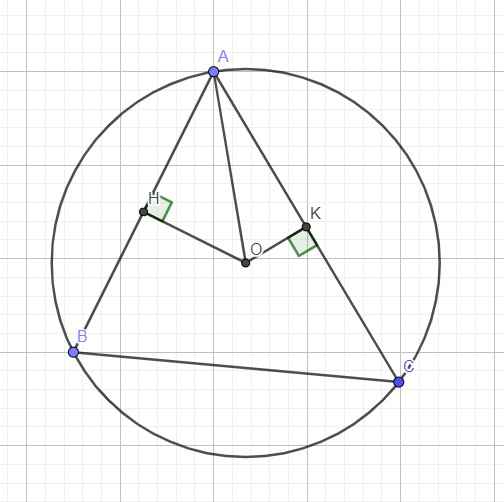
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) \(\Rightarrow OH=2\sqrt{2}\)

Áp dụng định lý Pitago cho tam giác OAH:

\(AH=\sqrt{OA^2-OH^2}=\sqrt{3^2-\left(2\sqrt{2}\right)^2}=1\)

\(\Rightarrow AB=2AH=2\left(cm\right)\)

Gọi K là trung điểm AC \(\Rightarrow OK\perp AC\Rightarrow OK=\dfrac{\sqrt{11}}{2}\)

Áp dụng định lý Pitago cho tam giác AOK:

\(AK=\sqrt{OA^2-OK^2}=\sqrt{3^2-\left(\dfrac{\sqrt{11}}{2}\right)^2}=2,5\left(cm\right)\)

\(\Rightarrow AC=2AK=5\left(cm\right)\)

Answer 2

Hình vẽ (chỉ mang tính chất minh họa):