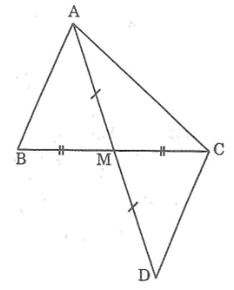
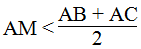Vẽ điểm D sao cho M là trung điểm của AD
\(\Delta AMB=\Delta DMC\left(c.g.c\right)\) nên \(AB=CD\)
Xét \(\Delta ACD:AD< AC+CD\) nên \(AD< AC+AB\)
Do \(AD=2AM\) nên \(2AM< AC+AB\)
Suy ra \(AM< \dfrac{AB+AC}{2}\)
Trên tia đối của tia AM lấy điểm D sao cho MA = MD.
Xét ΔAMB và ΔDMC, ta có:
MA = MD (theo cách vẽ)
∠(AMB) = ∠(DMC) (đối đỉnh)
MB = MC (gt)
Suy ra: ΔAMB = ΔDMC (c.g.c)
Suy ra: AB = CD (hai cạnh tương ứng)
Trong ΔACD, ta có: AD < AC + CD
(bất đẳng thức tam giác)
Suy ra: AD < AC + AB
Mà AD = AM + MD = 2AM
Suy ra: 2AM < AC + AB hay
Trên tia đối của tia AM lấy điểm D sao cho MA = MD.
Xét ΔAMB và ΔDMC, ta có:
MA = MD (theo cách vẽ)
∠(AMB) = ∠(DMC) (đối đỉnh)
MB = MC (gt)
Suy ra: ΔAMB = ΔDMC (c.g.c)
Suy ra: AB = CD (hai cạnh tương ứng)
Trong ΔACD, ta có: AD < AC + CD
(bất đẳng thức tam giác)
Suy ra: AD < AC + AB
Mà AD = AM + MD = 2AM
Suy ra: 2AM < AC + AB hay