a: góc ABC+góc ACB=180-60=120 độ
=>góc OBC+góc OCB=60 độ
=>góc BOC=120 độ
b: góc A+góc OBA+góc OCA
=60+30+30
=120 độ
=góc BOC
Đúng 0
Bình luận (0)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Bài 7: Định lí
Các câu hỏi tương tự
cho tam giác ABC điểm O nằm trong tam giác tia AO cắt BC tại điểm I
a) so sánh góc BOI và góc BAI
b)so sánh góc BOC và góc BAC
c) nếu góc BAC =90 độ thì góc BOC là góc tù
viết cả định lý với kết luận nữa nhé|
mk cảm ơn
Với hai góc kề bù, ta có định lí sau :
Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
a) Hãy vẽ hai góc xOy và yOx kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot của góc yOx và gọi số đo của góc xOy là m^0
b) Hãy viết giả thiết và kết luận của định lí
c) Hãy điền vào chỗ trống (.....) và sắp xếp bốn câu sau đây một cách hợp lí để chứng minh định lí trên
1) widehat{tOy}dfrac{1}{2}m^0 vì .............
2) widehat{tOy}dfrac{1}{2}left(180^0-m^0right) vì ..........
3) wideha...
Đọc tiếp
Với hai góc kề bù, ta có định lí sau :
Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
a) Hãy vẽ hai góc xOy và yOx' kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot' của góc yOx' và gọi số đo của góc xOy là \(m^0\)
b) Hãy viết giả thiết và kết luận của định lí
c) Hãy điền vào chỗ trống (.....) và sắp xếp bốn câu sau đây một cách hợp lí để chứng minh định lí trên
1) \(\widehat{tOy}=\dfrac{1}{2}m^0\) vì .............
2) \(\widehat{t'Oy}=\dfrac{1}{2}\left(180^0-m^0\right)\) vì ..........
3) \(\widehat{tOt'}=90^0\) vì .............
4) \(\widehat{x'Oy}=180^0-m^0\) vì ..........
Cho tam giác ABC , tia phân giác góc B và C cắt nhau ở I . Từ I kẻ đường thẳng song song với BC cắt AB ở D và AC ở E . Chứng minh: 1) Tính BAD và ADM . 2) Tính ADM .
Cho ΔABC cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D; M là trung điểm BC.a) Chứng minh: AD là phân giác của và A, M, D thẳng hàng. b) Qua B kẻ đường thẳng vuông góc AC cắt AC tại K, cắt AD tại I. Chứng minh: BC là đường trung trực của ID.
Đọc tiếp
Cho ΔABC cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D; M là trung điểm BC.
a) Chứng minh: AD là phân giác của 
b) Qua B kẻ đường thẳng vuông góc AC cắt AC tại K, cắt AD tại I. Chứng minh: BC là đường trung trực của ID.
Điền vào chỗ trống (.............) để chứng minh bài toán sau :
Gọi DI là tia phân giác của góc MDN. Gọi EDK là góc đối đỉnh của góc IDM.
Chứng minh rằng :
widehat{EDK}widehat{IDN}
GT :
KL :
Chứng minh (h.10)
widehat{IDM}widehat{IDN} (vì ................) (1)
widehat{IDM}widehat{EDK} (vì ...............) (2)
Từ (1) và (2) suy ra ...............
Đó là điều phải chứng minh
Đọc tiếp
Điền vào chỗ trống (.............) để chứng minh bài toán sau :
Gọi DI là tia phân giác của góc MDN. Gọi EDK là góc đối đỉnh của góc IDM.
Chứng minh rằng :
\(\widehat{EDK}=\widehat{IDN}\)
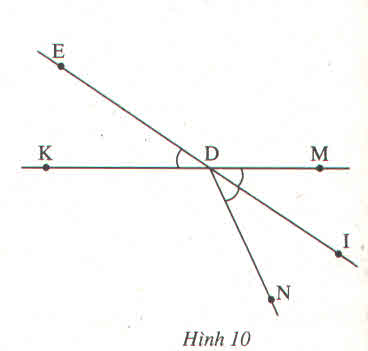
GT :
KL :
Chứng minh (h.10)
\(\widehat{IDM}=\widehat{IDN}\) (vì ................) (1)
\(\widehat{IDM}=\widehat{EDK}\) (vì ...............) (2)
Từ (1) và (2) suy ra ...............
Đó là điều phải chứng minh
Cho tam giác ABC cân tại A Trên tia đối của tia BC lấy điểm D Trên tia đối của tia CB lấy điểm E Sao cho BD=CE.Kẻ BH vuông góc AD (H thuộc AD),kẻ CK vuông góc AE (K thuộc AE) a,c/m BH=CK b, c/m tam giác AHB= tam giác AHC c,c/m BC//HK
cho góc nhọn xOy.trên hai canh OX và OY lần lượt lấy hai điểm A và B sao cho OA =OB.tia phân giác của góc XOY cắt ab tại I.
a/ chứng minh: oi là đường trung trực của AB
b/ Kẻ AD vuông góc với Oy (D thuộc Oy);C là giao điểm của AD với OI .Chứng minh BC vuông góc với Ox.
c/BC cắt Ox tại E. C hứng minh :DE song song với AB
Cho 2 góc xOy và mIn
Ox song song Im
Oy song song In
CM: 1. widehat{xOy}widehat{mIn} (Nếu 2 góc cùng nhọn hay cùng tù)
2. widehat{xOy}+widehat{mIn} 180^0( Nếu có một góc nhọn và một góc tù)
Giúp mình với mình sắp Kt rồi
Đọc tiếp
Cho 2 góc xOy và mIn
Ox\(\) song song Im
Oy song song In
CM: 1. \(\widehat{xOy}=\widehat{mIn}\) (Nếu 2 góc cùng nhọn hay cùng tù)
2. \(\widehat{xOy}+\widehat{mIn}\) =\(180^0\)( Nếu có một góc nhọn và một góc tù)
Giúp mình với mình sắp Kt rồi
Chứng minh rằng :
Nếu hai góc nhọn xOy và x'O'y' có Ox //O'x' ; Oy // O'y' thì :
\(\widehat{xOy}=\widehat{x'O'y'}\)
Hướng dẫn : Sử dụng tính chất của hai đường thẳng song song