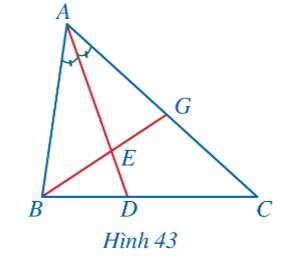
Từ B kẻ đường thẳng song song với AC, cắt AD tại K.
Vì \(BK//AC\) nên theo hệ quả của định lý Thales, ta có: \(\frac{{DB}}{{DC}} = \frac{{BK}}{{AC}}\)
Mà \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) nên \(\frac{{BK}}{{AC}} = \frac{{AB}}{{AC}} \Rightarrow AB = BK\)
Khi đó tam giác ABK cân tại B nên \(\widehat {BAK} = \widehat {BKA}\)
Mà \(BK//AC\) nên \(\widehat {BKA} = \widehat {KAC}\)
\( \Rightarrow \widehat {BAK} = \widehat {KAC}\)
Vậy AD là đường phân giác trong tam giác ABC.