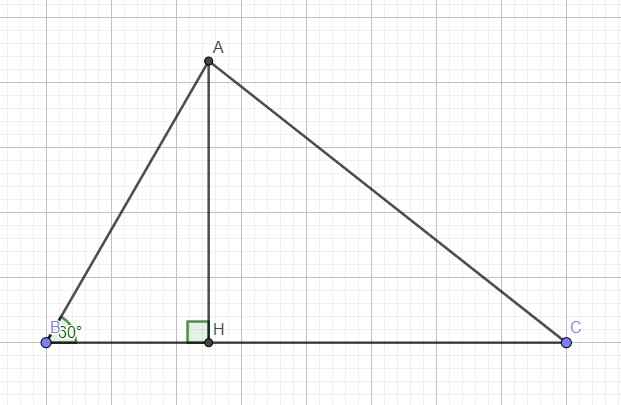
Kẻ đường cao AH ứng với BC
Đặt \(AB=x\) với \(0< x< 12\Rightarrow AC=12-x\)
Đặt \(BH=y\Rightarrow CH=8-y\) (với \(0< y< 8\))
Trong tam giác vuông ABH ta có:
\(cosB=\dfrac{BH}{AB}\Rightarrow BH=AB.cosB=\dfrac{x}{2}\Rightarrow y=\dfrac{x}{2}\)
\(\Rightarrow CH=8-y=8-\dfrac{x}{2}\)
\(sinB=\dfrac{AH}{AB}\Rightarrow AH=AB.sinB=\dfrac{x\sqrt{3}}{2}\)
Áp dụng Pitago cho tam giác vuông ACH:
\(AC^2=AH^2+CH^2\Leftrightarrow\left(12-x\right)^2=\left(\dfrac{x\sqrt{3}}{2}\right)^2+\left(8-\dfrac{x}{2}\right)^2\)
\(\Leftrightarrow16x-80=0\Rightarrow x=5\)
\(\Rightarrow AC=12-x=7\)
Vậy \(AB=5cm,AC=7cm\)