Cho tam giác \(ABC\) có \(BC\) bằng 30cm. Trên đường cao \(AH\) lấy các điểm \(K,I\) sao cho \(AK = KI = IH\). Qua \(I\) và \(K\) vẽ các đường \(EF//BC,MN//BC\left( {E,M \in AB;F,N \in AC} \right)\).
a) Tính độ dài các đoạn thẳng \(MN\) và \(EF\).
b) Tính diện tích tứ giác \(MNFE\) biết rằng diện tích tam giác \(ABC\) là \(10,8d{m^2}\).
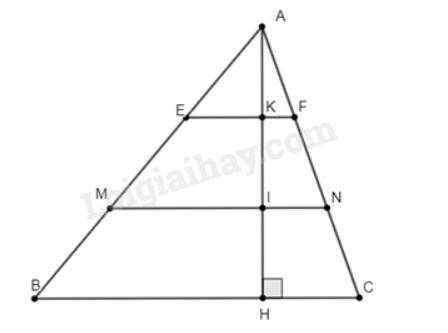
a) Vì \(AK = KI = IH \Rightarrow AK = \frac{1}{3}AH;AI = \frac{2}{3}AH\).
Vì \(EF//BC \Rightarrow EK//BH;MN//BC \Rightarrow MI//BH\)
Xét tam giác \(ABH\) ta có \(EK//BH\), theo định lí Thales ta có:
\(\frac{{AE}}{{AB}} = \frac{{AK}}{{AH}} = \frac{1}{3}\)
Xét tam giác \(ABH\) ta có \(MI//BH\), theo định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{AI}}{{AH}} = \frac{2}{3}\)
Xét tam giác \(ABC\) ta có \(EF//BC\), theo hệ quả của định lí Thales ta có:
\(\frac{{AE}}{{AB}} = \frac{{EF}}{{BC}} = \frac{1}{3} \Rightarrow \frac{{EF}}{{30}} = \frac{1}{3} \Rightarrow EF = \frac{{30.1}}{3} = 10\)
Xét tam giác \(ABC\) ta có \(MN//BC\), theo hệ quả của định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{MN}}{{BC}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{30}} = \frac{2}{3} \Rightarrow EF = \frac{{30.2}}{3} = 20\)
Vậy \(EF = 10cm;MN = 20cm\).
b) Đổi \(10,8d{m^2} = 1080c{m^2}\)
Diện tích tam giác \(ABC\) là:
\({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}AH.30 = 1080\left( {c{m^2}} \right)\)
\( \Rightarrow AH = 1080.2:30 = 72cm\)
Ta có: \(AH \bot BC \Rightarrow AH \bot MN\) (quan hệ từ vuông góc đến song song)
Do đó, \(KI \bot MN\)
Mà \(KI = \frac{1}{3}AH \Rightarrow KI = \frac{1}{3}.72 = 24cm\)
Tứ giác \(MNFE\) có \(MN//EF\) (cùng song song với \(BC\)) nên tứ giác \(MNFE\) là hình thang.
Lại có: \(KI \bot MN \Rightarrow KI\)là đường cao của hình thang.
Diện tích hình thang \(MNFE\) là:
\({S_{MNFE}} = \frac{1}{2}\left( {EF + MN} \right).KI = \frac{1}{2}.\left( {10 + 20} \right).24 = 360\left( {c{m^2}} \right)\)
Vậy diện tích tứ giác \(MNFE\) là \(360c{m^2}\).
a:
Xét ΔABH có EK//BH
nên EK/BH=AK/AH=1/3
Xét ΔAHB có MI//BH
nên MI/BH=2/3
Xét ΔABC có MN//BC
nên AM/AB=MN/BC
=>MN/30=2/3
=>MN=20(cm)
Xét ΔABC có EF//BC
nên EF/BC=AE/AB=1/3
=>EF=10(cm)
b: S ABC=1/2*AH*BC
=>1/2*AH*30=1080
=>AH=1080/15=72(cm)
KI=1/3*AH=24(cm)
S MNFE=1/2*(EF+MN)*KI=360cm2