Bài giải:
Cho parabol
và đường thẳng (m là tham số).
a) Vẽ parabol
Ta có bảng giá trị:
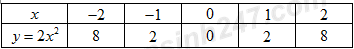
Vậy đồ thị hàm số là đường cong đi qua các điểm:
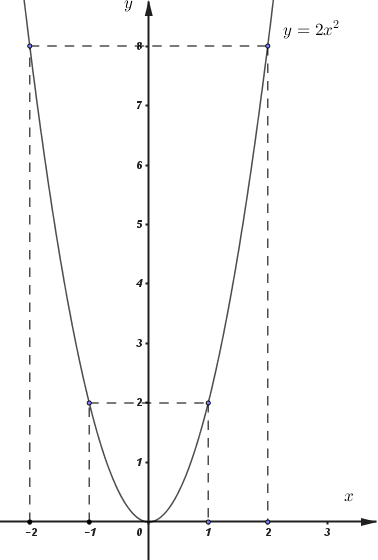
b) Với những giá trị nào của thì và chỉ có một điểm chung. Tìm tọa độ điểm chung đó.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
Số giao điểm của đồ thị (P) và đường thẳng (d) cũng chính là số nghiệm của phương trình (*)
Đồ thị hàm số và chỉ có một điểm chung
b) Với những giá trị nào của
thì và chỉ có một điểm chung. Tìm tọa độ điểm chung đó.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
Số giao điểm của đồ thị (P) và đường thẳng (d) cũng chính là số nghiệm của phương trình (*)
Đồ thị hàm số và chỉ có một điểm chung phương trình có nghiệm kép
Với ta có:

