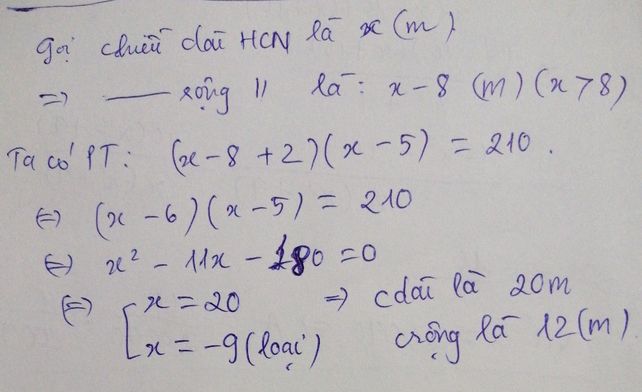- Gọi chiều dài hình chữ nhật ban đầu là a (m) (a>8)
=> chiều rộng hình chữ nhật ban đầu là: a-8 (m)
- Chiều dài mới của hình chữ nhật là: a-5 (m)
- Chiều rộng mới của hình chữ nhật là: a-8+2=a-6 (m)
=> diện tích mới hình chữ nhật là: (a-6)(a-5) (m\(^2\))
=> pt: (a-6)(a-5)=210
<=> (bạn tự giải nhé) a=20 (tmđk) hoặc a=-9 (ktmđk)
=> chiều dài ban đầu là: 20 (m) ; chiều rộng ban đầu là: 20-8=12 (m)
1, giải theo hệ phương trình
2, giải theo phương trình
tôi muốn giải cách 1
Gọi chiều rộng mảnh đất lúc đầu là \(\text{x (m)}\\\), chiều dài là \(\text{x + 8 (m), x > 0}\).
Diện tích mảnh đất ban đầu là \(x\left(x+8\right)m^2\)
Chiều dài mảnh đất lúc sau là \(\text{x + 8 - 5 = x+3}\left(m\right)\), chiều rộng mảnh đất lúc sau là \(\text{x +2 (m)}\). Diện tích mảnh đất lúc sau là \(\text{(x +3)(x + 2)}\) m2.
Theo bài ra ta có: \(\text{(x +3)(x + 2)}\) \(\text{= 210}\).
Giải phương trình ta được: \(x^2+5x-204=0\).
\(\Rightarrow\left\{{}\begin{matrix}x_{ }=12\left(tm\right)\\x_{ }=17\left(ktm\right)\end{matrix}\right.\)
Chiều rộng bằng 12m \(\rightarrow\) Chiều dài bằng 20m
\(\Rightarrow S=12.20=240m^2\)