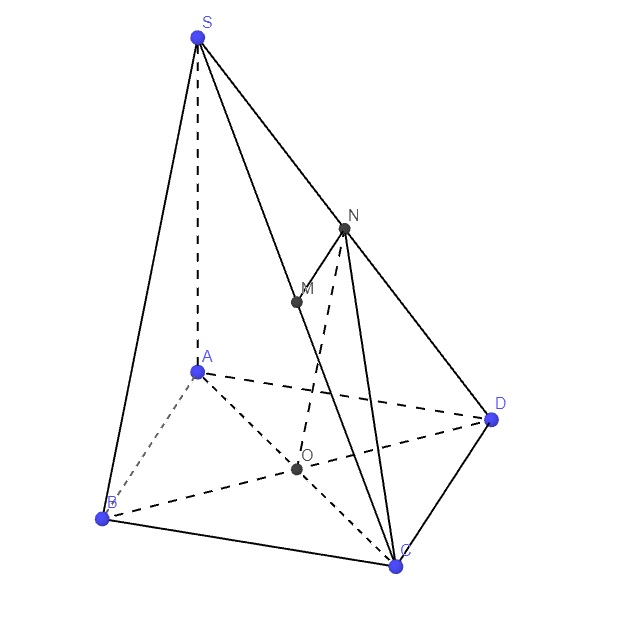
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\\BD\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp BD\)
Lại có \(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow BD\perp\left(SAC\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\) (1)
M là trung điểm SC, N là trung điểm SD \(\Rightarrow\) MN là đường trung bình tam giác SCD
\(\Rightarrow MN||CD\) (2)
(1);(2) \(\Rightarrow MN\perp\left(SAD\right)\)
Gọi O là tâm đáy \(\Rightarrow ON\) là đường trung bình tam giác SBD
\(\Rightarrow ON||SB\Rightarrow\widehat{\left(SB,CN\right)}=\widehat{\left(ON,CN\right)}=\widehat{ONC}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
\(ON=\dfrac{1}{2}SB\Rightarrow ON=a\)
\(OC=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
\(SD=\sqrt{SA^2+AD^2}=2a\Rightarrow ND=\dfrac{1}{2}SD=a\)
\(\Rightarrow CN=\sqrt{CD^2+ND^2}=a\sqrt{2}\)
\(cos\widehat{ONC}=\dfrac{ON^2+CN^2-OC^2}{2ON.CN}=\dfrac{5\sqrt{2}}{8}\)
\(\Rightarrow\widehat{ONC}\approx27^053'\)