Chà, bài này dựng xong hình là xong thôi (tính toán đơn giản bằng Talet)
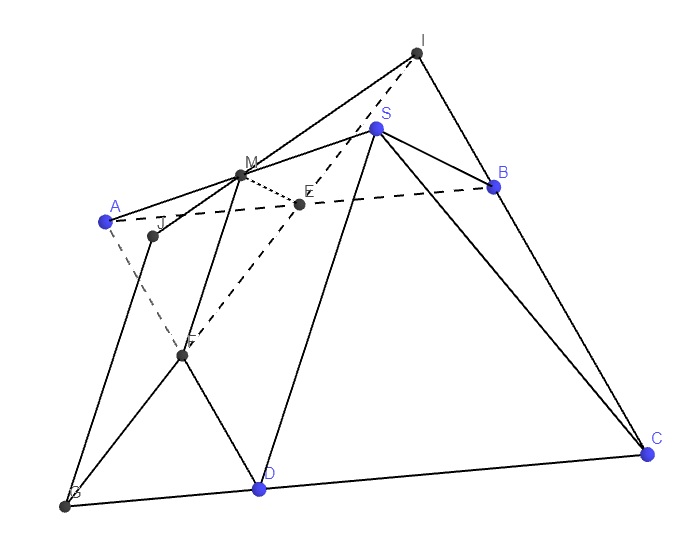
Đầu tiên là dựng mp qua M và song song (SBD): qua M kẻ các đường thẳng song song SB, SD lần lượt cắt AB, AD tại E và F
Nối EF kéo dài cắt BC tại I và CD tại G
Qua G kẻ đường thẳng song song MF (hoặc SD) cắt MI kéo dài tại J
Talet cho ta: \(\dfrac{MI}{MJ}=\dfrac{IF}{GF}\)
Mà \(\dfrac{GF}{GI}=\dfrac{DF}{BI}=\dfrac{\dfrac{1}{2}AD}{BC+\dfrac{1}{2}BC}=...\)
Vậy là xong