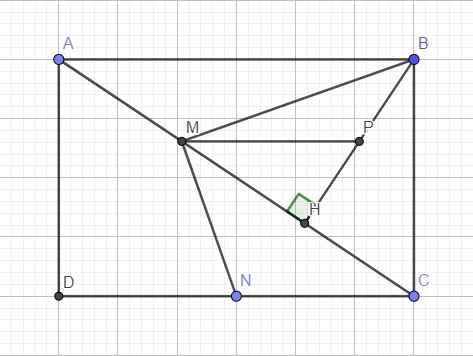
Áp dụng hệ thức lượng trong tam giác vuông ABC với đường cao BH:
\(AB^2=AH.AC\) (1)
Mặt khác ABCD là hình chữ nhật nên: \(\left\{{}\begin{matrix}AB=CD\\AC=BD\end{matrix}\right.\) (2)
(1); (2) \(\Rightarrow CD^2=AH.BD\)
b. Gọi P là trung điểm BH
\(\Rightarrow MP\) là đường trung bình tam giác ABH \(\Rightarrow\left\{{}\begin{matrix}MP||AB||CD\\MP=\dfrac{1}{2}AB\end{matrix}\right.\)
Mà \(NC=\dfrac{1}{2}CD\Rightarrow\left\{{}\begin{matrix}NC||MP\\NC=MP\end{matrix}\right.\) \(\Rightarrow MNCP\) là hbh
\(\Rightarrow MN||CP\) (3)
Do MP song song AB, mà AB vuông góc BC \(\Rightarrow MP\perp BC\)
\(\Rightarrow\) P là trực tâm tam giác BCM
\(\Rightarrow CP\perp MB\) (4)
(3);(4) \(\Rightarrow MN\perp MB\)