THAM KHẢO:
Các nửa mặt phẳng chia không gian thành 4 phần
Các nửa mặt phẳng chung bờ d là (P1), (P2), (Q1), (Q2)
=>Chia thành 4 phần
THAM KHẢO:
Các nửa mặt phẳng chia không gian thành 4 phần
Các nửa mặt phẳng chung bờ d là (P1), (P2), (Q1), (Q2)
=>Chia thành 4 phần
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\).
a) Trong trường hợp \(a\) vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và một đường thẳng \(b\) tuỳ ý trong \(\left( P \right)\).
b) Trong trường hợp \(a\) không vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và đường thẳng \(a'\) là hình chiếu vuông góc của \(a\) trên \(\left( P \right)\).
Cho hình lập phương \(ABCD.A'B'C'D'\). Tính góc giữa các đường thẳng sau đây với mặt phẳng \(\left( {ABCD} \right)\):
a) \(AA'\);
b) \(BC'\);
c) \(A'C\).
Cho hình chóp cụt lục giác đều \(ABCDEF.A'B'C'D'E'F'\) với \(O\) và \(O'\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\frac{a}{2},OO' = a\)
a) Tìm góc giữa cạnh bên và mặt đáy.
b) Tìm góc phẳng nhị diện \(\left[ {O,AB,A'} \right];\left[ {O',A'B',A} \right]\).
Cho hình chóp tứ giác đều \(S.ABCD\) có \(O\) là tâm của đáy và có tất cả các cạnh bằng nhau.
a) Tìm góc giữa đường thẳng \(SA\) và \(\left( {ABCD} \right)\).
b) Tim góc phẳng nhị diện \(\left[ {A,SO,B} \right];\left[ {S,AB,O} \right]\).
Cho hình chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy và có tất cả các cạnh đều bằng \(a\). Xác định và tính góc phẳng nhị diện:
a) \(\left[ {S,BC,O} \right]\);
b) \(\left[ {C,SO,B} \right]\).
Cho tứ diện đều \(ABCD\). Vẽ hình bình hành \(BCED\).
a) Tìm góc giữa đường thẳng \(AB\) và \(\left( {BCD} \right)\).
b) Tim góc phẳng nhị diện \(\left[ {A,CD,B} \right];\left[ {A,CD,E} \right]\).
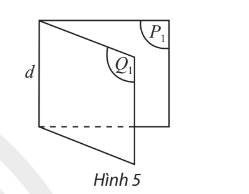
Cho góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\). Gọi \(O\) là một điểm tuỳ ý trên \(d\). \(Ox\) là tia nằm trong \(\left( P \right)\) và vuông góc với \(d\), \(Oy\) là tia nằm trong \(\left( Q \right)\) và vuông góc với \(d\) (Hình 6).
a) Nêu nhận xét về vị trí tương đối giữa \(d\) và \(mp\left( {Ox,Oy} \right)\).
b) Nêu nhận xét về số đo của góc \(xOy\) khi \(O\) thay đổi trên \(d\).
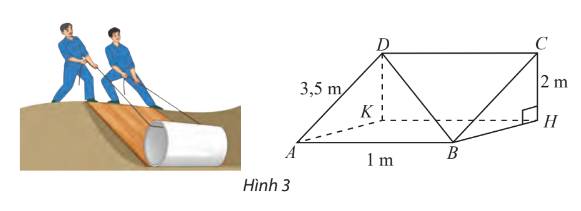
Một tấm ván hình chữ nhật \(ABCD\) được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu 2 m. Cho biết \(AB = 1\,m,AD = 3,5{\rm{ }}m\). Tính góc giữa đường thẳng \(BD\) và đáy hồ.
Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135°. Tính số mét khối đất cần phải di chuyển ra khỏi hầm.