THAM KHẢO:

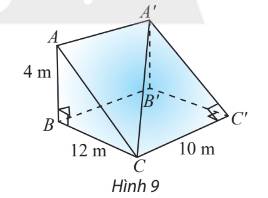
a) Vì AA′⊥(ABCD) nên góc giữa đường thẳng AA' và (ABCD) là \(90^0\)
b) CC′⊥(ABCD) nên C là hình chiếu vuông góc của C' lên (ABCD).
Suy ra góc giữa BC' và (ABCD) là \(\widehat{C'BC}\)=\(45^O\) (Vì BCC'C' là hình vuông)c) Gọi cạnh của hình lập phương là a
Ta có: AC=\(a\sqrt{2}\),tan \(\widehat{ACA'}\)=\(\dfrac{1}{\sqrt{2}}\) nên \(\widehat{ACA'}\)=\(35^O\)
AA′⊥(ABCD) nên A là hình chiếu vuông góc của A' lên (ABCD)
Suy ra góc giữa A'C và (ABCD) là \(\widehat{ACA'}\)=\(35^O\)