Question

Cho hai điểm B, C cố định (BC không phải đường kính) trên đường tròn (O), điểm A di động trên (O). Khi A di động trên (O) thì trực tâm tam giác ABC di động như thế nào?

Answer 1

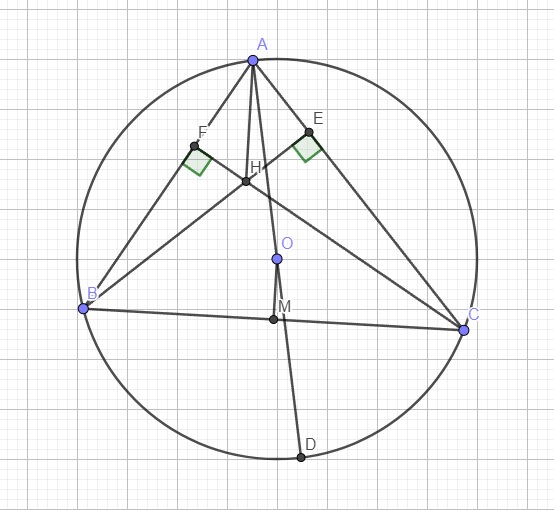
Gọi H là trực tâm, M là trung điểm BC \(\Rightarrow M\) cố định

Tới đây ta có 1 bài toán hình phẳng hết sức quen thuộc: kẻ đường kính AD, từ đó dễ dàng chứng minh BHCD là hình bình hành, từ đó suy ra M; H; D thẳng hàng đồng thời M là trung điểm HD

\(\Rightarrow\) OM là đường trung bình tam giác AHD

\(\Rightarrow\overrightarrow{AH}=2\overrightarrow{OM}\) cố định

\(\Rightarrow H\) là ảnh của A qua phép tịnh tiến vecto \(2\overrightarrow{OM}\)

\(\Rightarrow\) Trực tâm H di động trên đường tròn (O') là ảnh của (O) qua phép tịnh tiến \(2\overrightarrow{OM}\)

Answer 2