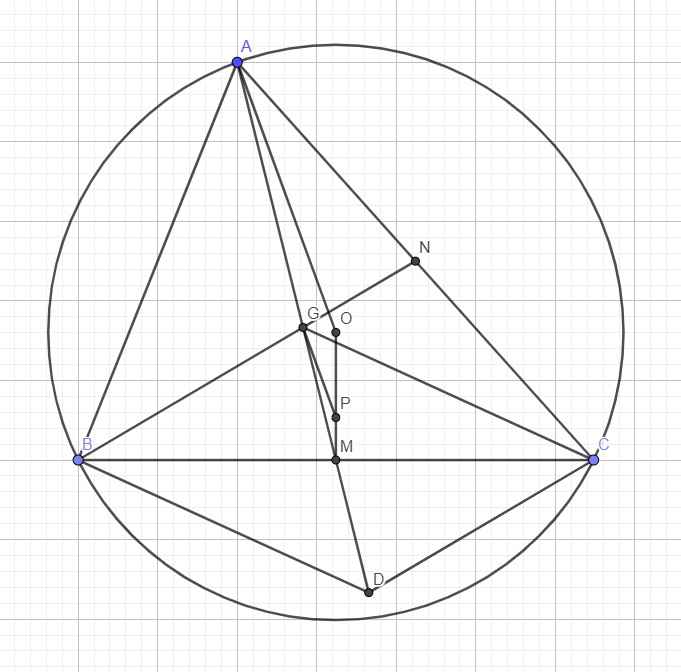
Nối OA, gọi M là trung điểm BC \(\Rightarrow\) OM cố định
Qua G kẻ đường thẳng song song OA cắt OM tại P
Trong tam giác OAM, theo định lý Talet:
\(\dfrac{GP}{OA}=\dfrac{PM}{OM}=\dfrac{GM}{AM}=\dfrac{1}{3}\)
Ta có những điều sau:
\(PM=\dfrac{1}{3}OM\) , mà O cố định, M cố định \(\Rightarrow\) P cố định
\(GP=\dfrac{1}{3}OA\Rightarrow GP=\dfrac{R}{3}\)
P cố định, độ dài \(\dfrac{R}{3}\) cố định
\(\Rightarrow\) Quỹ tích G là đường tròn (P) tâm P bán kính \(r=\dfrac{R}{3}\) (1)
Mặt khác BGCD là hình bình hành \(\Rightarrow\) D đối xứng G qua M (2)
(1);(2) \(\Rightarrow\) quỹ tích D là ảnh của đường tròn (P) qua phép đối xứng tâm M