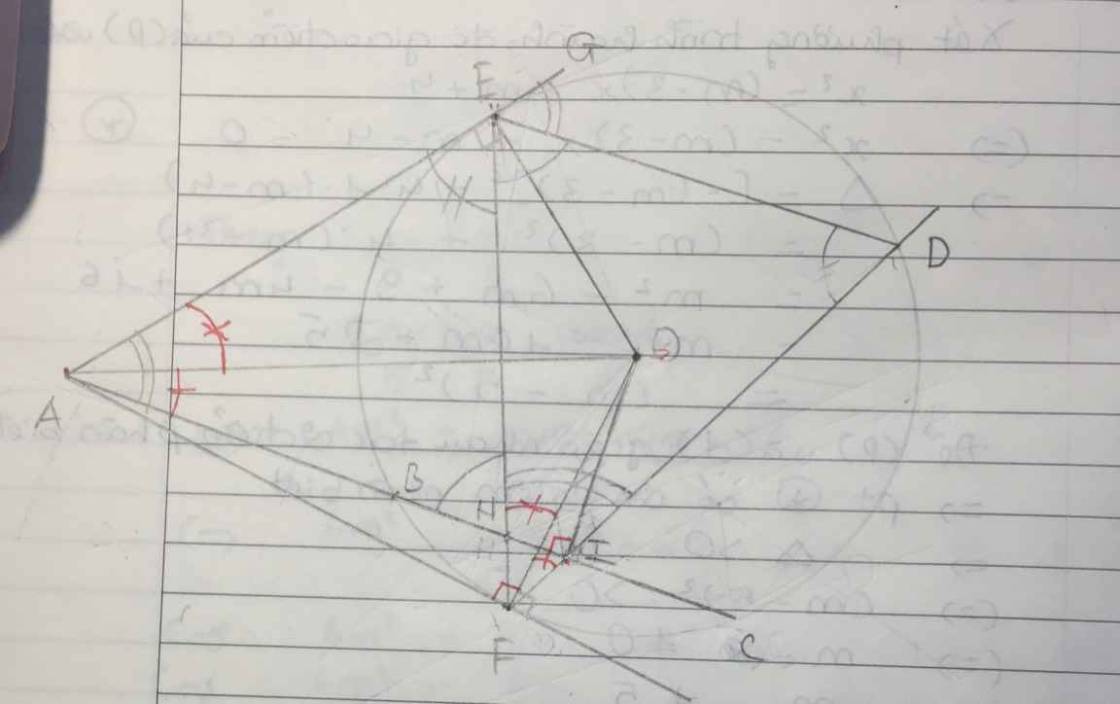
a: Xét tứ giác AECO có
\(\widehat{EAO}+\widehat{ECO}=90^0+90^0=180^0\)
=>AECO là tứ giác nội tiếp
=>A,E,C,O cùng thuộc một đường tròn
b: Ta có: ΔOBC cân tại O
mà OF là đường trung tuyến
nên OF là tia phân giác của góc COB
Xét ΔCOF và ΔBOF có
OC=OB
\(\widehat{COF}=\widehat{BOF}\)
OF chung
Do đó: ΔOCF=ΔOBF
=>\(\widehat{OCF}=\widehat{OBF}\)
mà \(\widehat{OCF}=90^0\)
nên \(\widehat{OBF}=90^0\)
=>FB là tiếp tuyến của (O)
c: Xét (O) có
EA,EC là các tiếp tuyến
=>EA=EC
=>E nằm trên đường trung trực của AC(1)
Ta có: OA=OC
=>O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra OE là đường trung trực của AC
=>OE\(\perp\)AC tại H và H là trung điểm của AC
Xét ΔAEO vuông tại A có AH là đường cao
nên \(OH\cdot OE=OA^2\)
=>\(4\cdot OH\cdot OE=4\cdot OA^2=\left(2\cdot OA\right)^2=AB^2\)