(3,5điểm) Cho đường tròn O,R; đường kính AB. Kẻ tiếp tuyến Ax và lấy trên tiếp tuyến môt điểm C sao cho AC >R . Từ C kẻ tiếp tuyến tiếp xúc với (O) tại E.
a) Chứng minh rằng 4 điểm A C E O cùng nằm trên một đường tròn.
b) Chứng minh BE OC // .
c) Đường thẳng vuông góc với AB ở O cắt tia BE tại D. Chứng minh tứ giác OBDClà hình bình hành. d) Biết AD cắt OC tại F, CE cắt OD tại G, CD và OE kéo dài cắt nhau tại H. Chứng minh 3 điểm F G H thẳng hàng
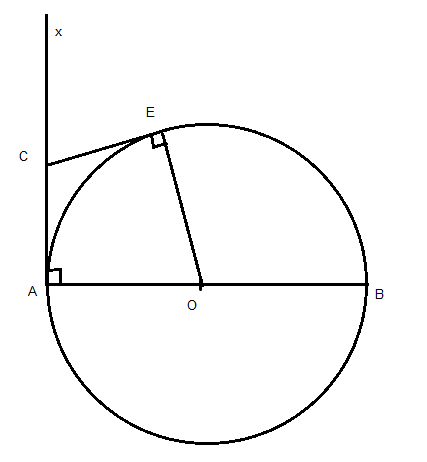
a) xét tứ giác ACEO có :
\(\widehat{CAO}\) = 900 ( tính chất tiếp tuyến )
\(\widehat{CEO}\) = 900 ( tính chất tiếp tuyến )
ta có : \(\widehat{CAO}\) + \(\widehat{CEO}\) = 1800
mà hai góc này nằm ở vị trí đối nhau
==> tứ giác ACEO nội tiếp
hay bốn điểm A C E O cùng thuộc một đường tròn


