Question

Cho \(\Delta ABC\) vuông tại A có đường cao AH. Goi D,E lần lượt là hình chiếu của H lên cạnh AB,AC
a) Chứng minh: \(\widehat{ADE}=\widehat{ACB}\) 

b) Gọi K là điểm đối xứng của A qua H và F là trung điểm của AB. Chứng minh \(CF\perp KE\)

Answer 1

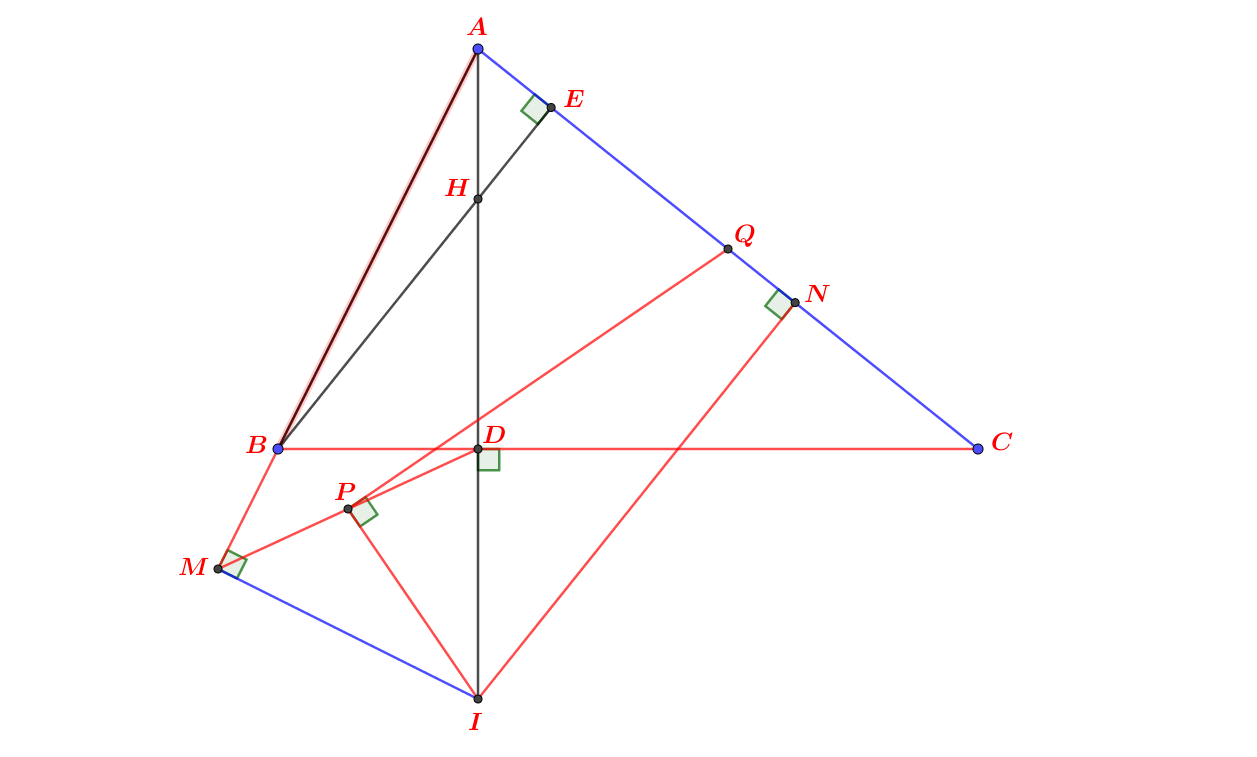
a: ΔHAB vuông tại H có HD vuông góc AB

nên AD*AB=AH^2

ΔAHC vuông tại H co HE vuông góc AC

nên AE*AC=AH^2

=>AD*AB=AE*AC

=>AD/AC=AE/AB

=>ΔADE đồng dạng với ΔACB
=>góc ADE=góc ACB

b: Kẻ KI vuông góc AC

=>KI//HE

=>AE=EI

EI/KI=AE/2HE=AE/2AD

FA/AC=AB/2AC

AE/2AD=AB/2AC

=>EI/KI=FA/AC

=>ΔEIK đồng dạng với ΔFAC

Gọi giao của EK vơi FC là O

goc OEC=góc AFC

=>góc OEC+góc OCE=90 độ

=>EK vuông góc FC