\(32>4x-5\)
\(\Leftrightarrow4x-5-3x< 0\)
\(\Leftrightarrow x-5< 0\)
\(\Leftrightarrow x< 5\)
3x>4x-5
\(\Leftrightarrow\)3x-4x>-5
\(\Leftrightarrow\)-x>-5
\(\Leftrightarrow\)x<5
Vậy S={x|x<5}
Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào ? (kể ba bất phương trình có cùng tập nghiệm)
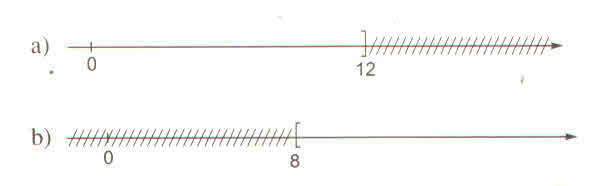
Đố :
Kiểm tra xem giá trị \(x=-2\) có là nghiệm của bất phương trình sau không ?
a) \(x+2x^2-3x^3+4x^4-5< 2x^2-3x^3+4x^4-6\)
b) \(\left(-0,001\right)x>0,003\)
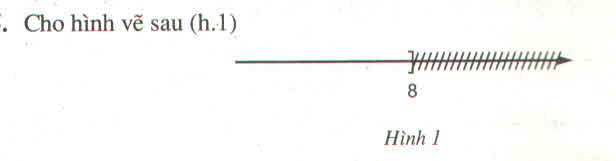
Bạn An cho rằng, hình vẽ đó biểu diễn tập nghiệm của bất phương trình \(2x\le16\), còn bạn Bình lại khẳng định hình vẽ đó là biểu diễn của tập nghiệm bất phương trình \(x+2\le10\)
Theo em bạn nào đúng ?
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số :
a) \(1,2x< -6\)
b) \(3x+4>2x+3\)
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số :
a) \(2x-3>0\)
b) \(3x+4< 0\)
c) \(4-3x\le0\)
d) \(5-2x\ge0\)
Cho bất phương trình \(x^2>0\) :
a) Chứng tỏ \(x=2;x=-3\) là nghiệm của bất phương trình đã cho
b) Có phải mọi giá trị của ẩn \(x\) đều là nghiệm của bất phương trình đã cho không ?
Hãy cho biết số nào trong các số \(\dfrac{2}{3};\dfrac{2}{7};-\dfrac{4}{5}\) là nghiệm của bất phương trình :
\(5-3x< \left(4+2x\right)-1\)
Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số :
a) \(2x-4< 0\)
b) \(3x+9>0\)
c) \(-x+3< 0\)
d) \(-3x+12>0\)
Nghiệm của bất phương trình
x(4x-4)-32>4x(x+1)
là ? (viết dạng x >3 hoặc x \(\ge\)3
