Cho ∆ABC vuông tại A có phân giác của góc ABC cắt AC tại D. Từ D vẽ đường thẳng song song BC cắt AB tại M. a) Giả sử AB = 6cm, AD = 3cm, CD = 5cm. Tính BC. Tính tỉ số diện tích của ∆AMD với ∆ABC b) Vẽ DE BC tại E. Chứng minh: ∆AMD ∽ ∆EDC. Từ đó suy ra: c) Từ C vẽ đường thẳng vuông góc với BD cắt BD tại I. Chứng minh: BC^2 = BD.BI + CD.CA
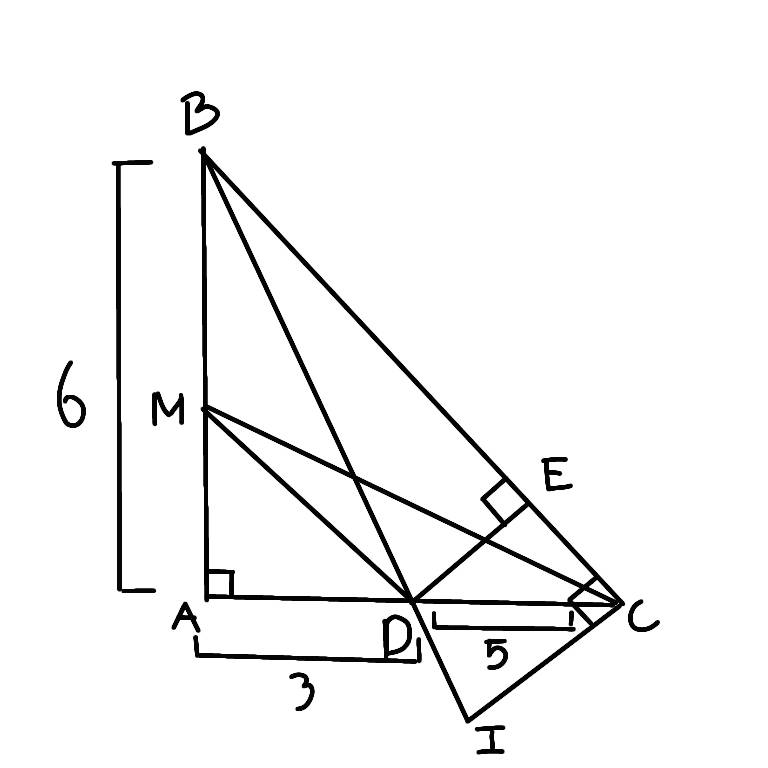a. Tính BC
BC^2 = AC^2 + AB^2
BC^2 = 6^2 + ( AD + DC )^2 = 8^2
BC^2 = 36 + 64 = 100
BC = căng bậc 100 = 10 cm
Tính tỉ số diện tích
Xét tam giác ABC có MD // BC
tam giác AMD ~ tam giác ABC
=>Diện tích tam giác AMD / Diện tích tam giác ABC = (AD/AC)^2=(3/8)^2=9/16 cm2
b.Xét tam giác AMD và tam giác EDC có
Góc MAD = góc CED = 90° (gt)
Góc D chung
=> tam giác AMD ~ tam giác EDC (g.g)
=>MD/AD = DC/EC
=>MD.EC=AD.DC
c. Xét tam giác BCI và tam giác BDE có
Góc BCI = Góc BED = 90°(gt)
Góc B chung
=> Tam giác BCI ~ tam giác BDE(g.g)
=> BC/BI = BD/BE
=> BC.BE = BI.BD(1)
Xét tam giác CBA và tam giác CDE có
Góc CAB = góc CED =90° (gt)
Góc C chung
=> Tam giác CBA ~ tam giác CDE(g.g)
=> CB/CA=CD/CE
=> CB.CE = CA.CD(2)
Từ (1) và (2) ta cộng cho 2 vế
=>BC.BE + CB.CE = BD.BI + CA.CD
=>(BE+CE)BC = BD.BI + CA.CD
=> BC.BC = BD.BI + CA.CD
=> BC^2 = BD.BI + CA.CD
đồng dạng từ đó suy ra CD.CA = CM.CB
đồng dạng
vuông cân
suy ra BM là phân giác của 