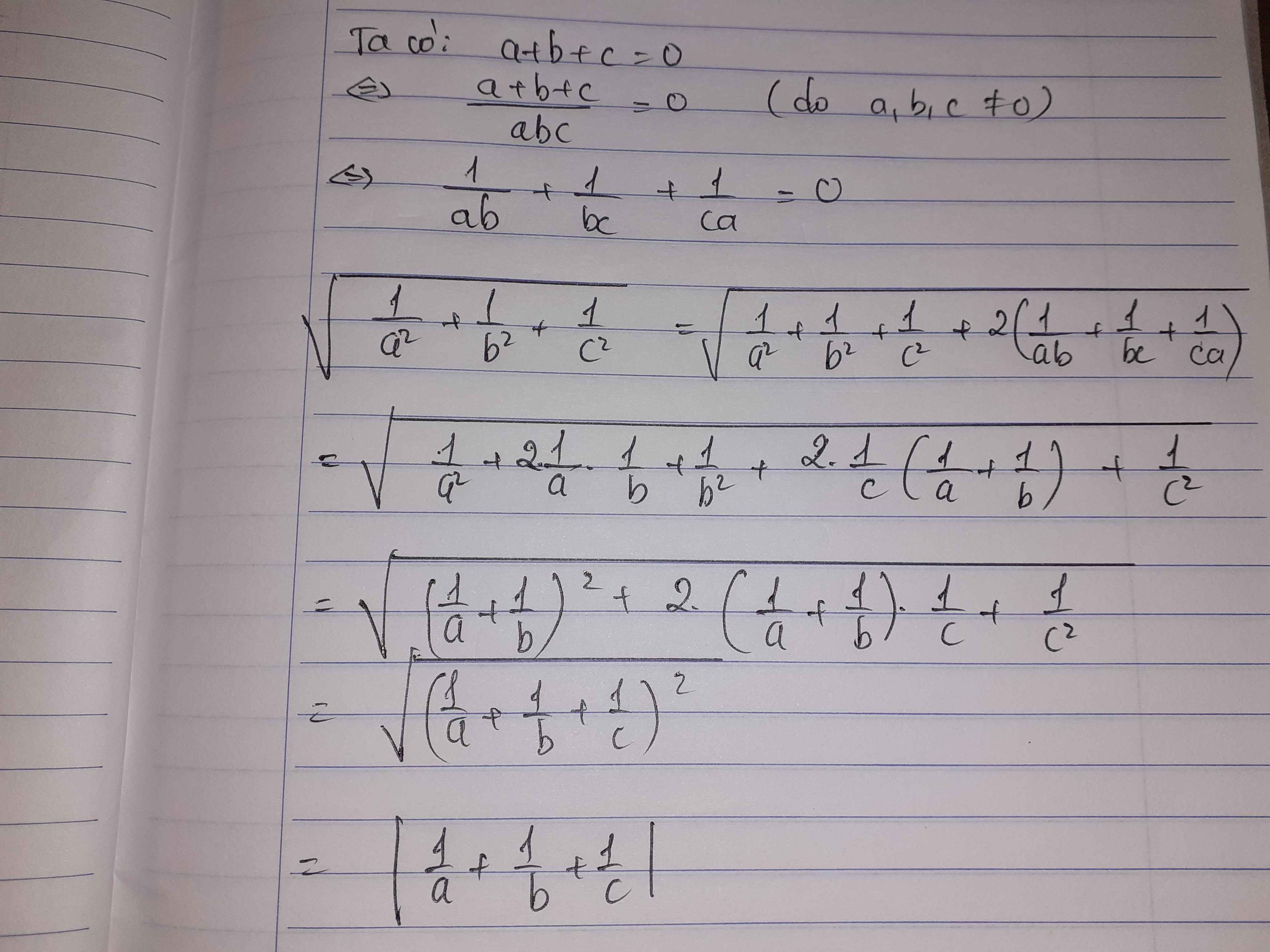Ta có: \(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\left(\dfrac{c}{abc}+\dfrac{b}{abc}+\dfrac{a}{abc}\right)}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\cdot\dfrac{a+b+c}{abc}}\)
\(=\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)