Question

Cho 3 điểm A,B,C cố định nằm trên 1 đthẳng d ( B nằm giữa A và C ) . Vẽ đtròn tâm O thay đổi nhưng luôn đi qua B và C (O nằm trên đthẳng d) . Kẻ AM và AN là các tiếp tuyến vs đtròn tâm O tại M và N . Gọi I là trung điểm của BC , AO cắt MN tại H và cắt đtròn tại P và Q (P nằm giữa A và O ) , BC cắt MN tại K

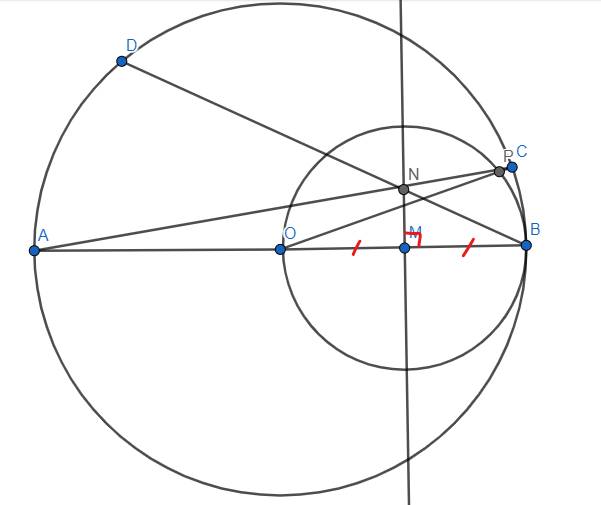
a, Cm điểm K cố định khi đtròn tâm O thay đổi

b, Gọi D là trung điểm HQ từ H kẻ đường vg góc vs MD cắt đường thẳng MP tại E . Cm P là trung điểm của ME

Answer 1

a) Xét \(\Delta AHK\) và \(\Delta AIO\) có:

\(\left\{{}\begin{matrix}\widehat{AHK}=\widehat{AIO}=90^o\\\widehat{HAK}-\text{góc chung}\end{matrix}\right.\)

\(\Rightarrow \Delta AHK\sim\Delta AIO(g.g)\)

\(\Rightarrow\frac{AH}{AK}=\frac{AI}{AO}\Rightarrow AI.AK=AH.AO\). (1)

Xét \(\Delta ANO\) vuông tại N có \(NH\perp AO\)

\(\Rightarrow AH.AO=AN^2\). (2)

Xét \(\Delta ANB\) và \(\Delta ACN\) có:

\(\left\{{}\begin{matrix}\widehat{BAN}-\text{góc chung}\\\widehat{ANB}=\widehat{ACN}=\left(\frac{1}{2}sđ\stackrel\frown{BN}\right)\end{matrix}\right.\)

\(\Rightarrow\Delta ANB\sim\Delta ACN(g.g)\)

\(\Rightarrow\frac{AN}{AB}=\frac{AC}{AN}\Rightarrow AN^2=AB.AC\). (3)

Từ (1), (2), (3) suy ra \(AI.AK=AB.AC\).

Mà A, B, C, I cố định nên độ dài AK cố định.

Mà K nằm trên tia AB nên K cố định.

Answer 2

Answer 3

b) Gọi T là trung điểm của MH.

Dễ dàng chứng minh được: \(\Delta MHQ\sim\Delta PHM(g.g)\).

Mà MD, PT lần lượt là hai đường trung tuyến của các cạnh tương ứng HQ và HM

Nên \(\widehat{TPM}=\widehat{DMQ}\).

Mặt khác do \(EH\perp MD\) và \(PM\perp MQ\) nên \(\widehat{DMQ}=\widehat{MEH}=90^o-\widehat{DMP}\).

Do đó \(\widehat{TPM}=\widehat{MEH}\Rightarrow PT//EH\).

Mà T là trung điểm của MH nên PT là đường trung bình của tam giác MEH.

Vậy P là trung điểm của ME.