Question

Bạn đã biết tỉ số lượng giác của một góc nhọn. Đối với góc tù thì sao?

Answer 1

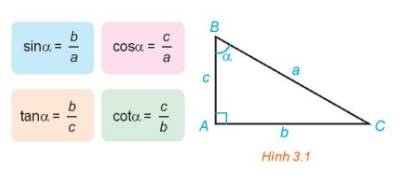
Góc \(\alpha \) cho trước,\({0^o} < \alpha  < {180^o}\).

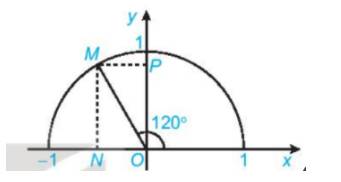
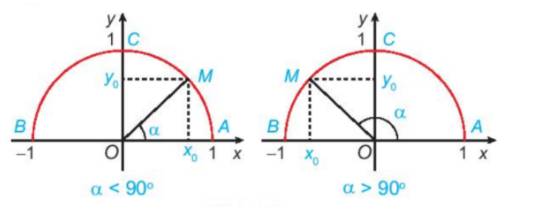
Trên nửa đường tròn đơn vị, vẽ điểm \(M({x_o};{y_o})\) sao cho \(\widehat {xOM} = \alpha .\)

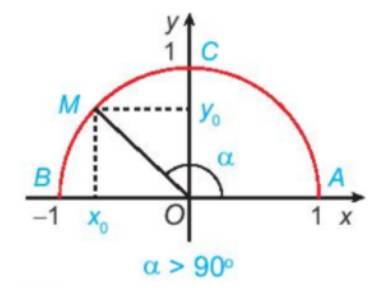
Khi đó:

\(\begin{array}{l}\sin \alpha  = {y_o};\\\cos \alpha  = {x_o};\\\tan \alpha  = \frac{{{x_o}}}{{{y_o}}}\;\;({y_o} \ne 0);\\\cot \alpha  = \frac{{{y_o}}}{{{x_o}}}\;\;({x_o} \ne 0).\end{array}\)

Answer 2

Ta có: \(\widehat{ACM}\) = \(\widehat{ACB}\) -- \(\widehat{MCB}\) = (180^o -- 90^o -- 45^o) -- (180^o -- 90^o -- 75^o) = 30^o

Xét △AMC:    \(\dfrac{MC}{\sin\widehat{MAC}}\) = \(\dfrac{AM}{\sin\widehat{ACM}}\)  (Định lí sin trong tam giác)

               ⇔   MC = \(\dfrac{AM.\sin\widehat{MAC}}{\sin\widehat{ACM}}\) = \(\dfrac{30.\dfrac{\sqrt{2}}{2}}{\dfrac{1}{2}}\) = 

Xét △BMC:     \(\sin\widehat{CMB}\) = \(\dfrac{CB}{CM}\)   ⇒  CB = CM.\(\sin75\) =