Question

Bài 3: Cho AABC vuông tại A có AH là đường cao, BD là đường phân giác ABC với D \in AC AH cắt BD tại I
a) Tính tỉ số (AI)/(AB) và (AD)/(AB)
b) Chứng minh AAID cân tại A.
c) Chứng minh (IH)/(BH) = (DC)/(BC)

 

Answer 1

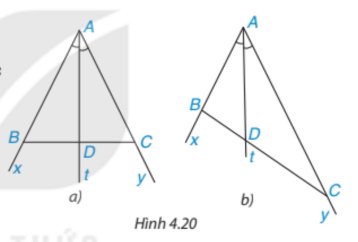
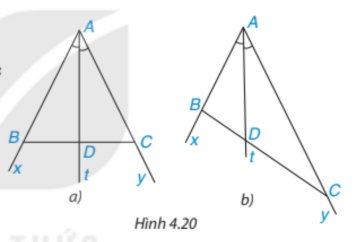
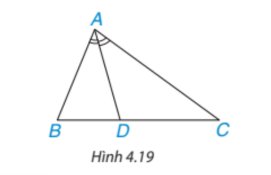
a: Xét ΔABC có BD là phân giác

nên \(\dfrac{AD}{AB}=\dfrac{DC}{BC}\)(2)

Xét ΔABH có BI là phân giác

nên \(\dfrac{AI}{AB}=\dfrac{IH}{BH}\)(1)

b: ta có: \(\widehat{ABD}+\widehat{ADB}=90^0\)(ΔABD vuông tại A)

\(\widehat{HBI}+\widehat{HIB}=90^0\)(ΔHBI vuông tại H)

mà \(\widehat{ABD}=\widehat{HBI}\)

nên \(\widehat{ADB}=\widehat{HIB}\)

=>\(\widehat{AID}=\widehat{ADI}\)

=>ΔADI cân tại A

=>AI=AD(3)

c: từ (1),(2),(3) suy ra \(\dfrac{IH}{BH}=\dfrac{DC}{BC}\)