Trong H.4.19, AD là đường phân giác của tam giác ABC. Hai tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\) có bằng nhau không?
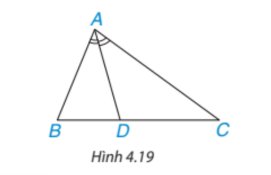
Trong H.4.19, AD là đường phân giác của tam giác ABC. Hai tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\) có bằng nhau không?

Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D.
Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\)
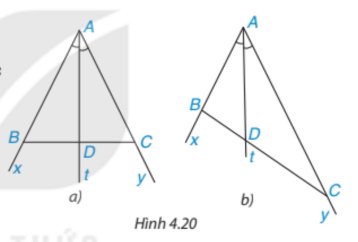
Theo đề bài, At là tia phân giác của góc xAy hay AD là tia phân giác của góc BAC.
Tam giác ABC cân tại A (vì AB = AC) có AD là tia phân giác của góc BAC nên AD cũng là đường trung tuyến của tam giác ABC.
Suy ra D là trung điểm của cạnh BC hay DB = DC nên \(\dfrac{{DB}}{{DC}} = 1\).
Vì AB = AC nên \(\dfrac{{AB}}{{AC}} = 1\)
Vậy khi lấy B và C sao cho AB = AC thì \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}\)
Trả lời bởi Hà Quang MinhCho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D
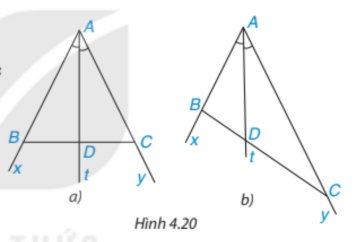
Khi lấy B và C sao cho AB = 2 cm và AC = 4 cm (H.4.20b), hãy dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC rồi so sánh hai tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\)
Dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC, ta được:
DB = 12 mm = 1,2 cm và DC = 24 mm = 2,4 cm.
Khi đó, \(\dfrac{{DB}}{{DC}} = \dfrac{{1,2}}{{2,4}} = \dfrac{1}{2};\dfrac{{AB}}{{AC}} = \dfrac{2}{4} = \dfrac{1}{2}\)
Vậy khi lấy B và C sao cho AB = 2 cm và AC = 4 cm thì \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}\)
Trả lời bởi Hà Quang MinhTính độ dài x trên Hình 4.23
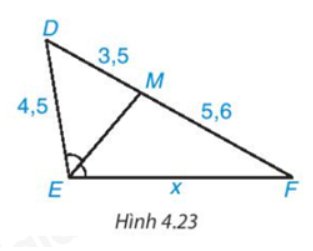
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).
Trả lời bởi Hà Quang MinhTính độ dài x trên Hình 4.24.
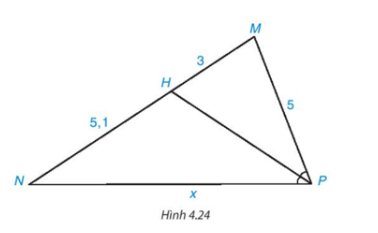
Trong Hình 4.24 có \(\widehat {MPH} = \widehat {NPH}\) nên PH là tia phân giác của \(\widehat {MPN}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{MP}}{{NP}} = \dfrac{{MH}}{{NH}}\) hay \(\dfrac{5}{x} = \dfrac{3}{{5,1}}\)
Suy ra \(x = \dfrac{{5.5,1}}{3} = 8,5\) (đvđd).
Vậy x = 8,5 (đvđd).
Trả lời bởi Hà Quang MinhCho tam giác ABC. Đường phân giác trong của góc A cắt BC tại D. Tính độ dài đoạn thẳng DC biết AB = 4,5 m; AC = 7,0 m và CB = 3,5 m (làm tròn kết quả đến hàng phần chục).
Theo đề bài, đường phân giác trong của góc A cắt BC tại D nên AD là tia phân giác của \(\widehat {BAC}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{AB}}{{AC}} = \dfrac{{DB}}{{DC}}\) hay \(\dfrac{{4,5}}{7} = \dfrac{{DB}}{{DC}}\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{{DB}}{{4,5}} = \dfrac{{DC}}{7} = \dfrac{{DB + DC}}{{4.5 + 7}} = \dfrac{{BC}}{{11,5}} = \dfrac{{3,5}}{{11,5}} = \dfrac{7}{{23}}\)
Suy ra \(DC = \dfrac{{7.7}}{{23}} = \dfrac{{49}}{{23}} \) ≈ 2,1 (m)
Vậy DC ≈ 2,1 m.
Trả lời bởi Hà Quang MinhNhà bạn Mai ở vị trí M, nhà bạn Dung ở vị trí D (Hình 4.25), biết rằng tứ giác ABCD là hình vuông và M là trung điểm của AB. Hai bạn đi bộ với cùng một vận tốc trên con đường MD để đến điểm I. Bạn Mai xuất phát lúc 7h. Hỏi bạn Dung xuất phát lúc mấy giờ để gặp bạn Mai lúc 7h30 tại điểm I?
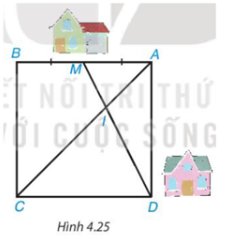
Theo đề bài, ABCD là hình vuông nên AB = AD và AC là tia phân giác của \(\widehat {BA{\rm{D}}}\)
Vì M là trung điểm của AB nên \(AM = BM = \dfrac{1}{2}AB = \dfrac{1}{2}A{\rm{D}}\) hay \(\dfrac{{AM}}{{A{\rm{D}}}} = \dfrac{1}{2}\)
Vì AC là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay AI là tia phân giác của \(\widehat {MA{\rm{D}}}\), áp dụng tính chất đường phân giác trong tam giác ADM, ta có:
\(\dfrac{{AM}}{{A{\rm{D}}}} = \dfrac{{IM}}{{I{\rm{D}}}} = \dfrac{1}{2}\) suy ra ID = 2IM.
Giả sử vận tốc đi bộ của bạn Mai và bạn Dung đều bằng nhau.
Theo đề bài, I là địa điểm gặp nhau nên bạn Mai đi theo quãng đường MI, bạn Dung đi theo quãng đường DI.
Vì quãng đường bạn Dung đi gấp 2 lần quãng đường bạn Mai đi và vận tốc đi bộ của hai bạn đều bằng nhau (giả sử) nên thời gian bạn Dung đi gấp 2 lần thời gian bạn Mai đi thì hai bạn mới gặp nhau tại địa điểm I.
Bạn Dung gặp bạn Mai lúc 7h30 nên thời gian bạn Mai đi trên quãng đường MI là:
7h30 – 7h = 30 phút.
Khi đó, thời gian bạn Dung đi là 1h. Do đó, bạn Dung xuất phát từ lúc:
7h30 – 1h = 6h30.
Vậy bạn Dung xuất phát lúc 6h30 để gặp bạn Mai lúc 7h30 tại điểm I.
Trả lời bởi Hà Quang Minh
Dựa vào tính chất đường phân giác trong tam giác với tam giác ABC có AD là phân giác của góc \(\widehat{BAC}\) , ta được: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\).
Trả lời bởi Hà Quang Minh