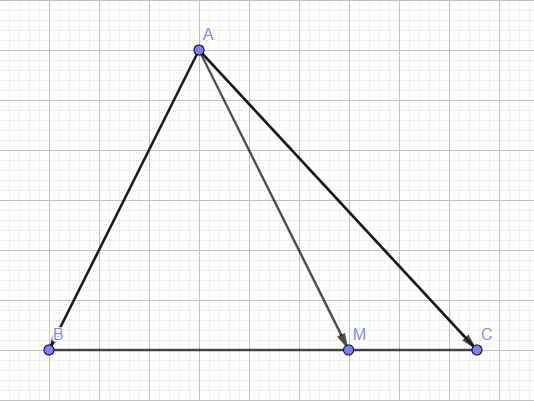
\(3BM=7CM=7\left(BC-BM\right)\Rightarrow10BM=7BC\)
\(\Rightarrow BM=\dfrac{7}{10}BC\Rightarrow\overrightarrow{BM}=\dfrac{7}{10}\overrightarrow{BC}\)
Ta có:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\dfrac{7}{10}\overrightarrow{BC}=\overrightarrow{AB}+\dfrac{7}{10}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{AB}-\dfrac{7}{10}\overrightarrow{AB}+\dfrac{7}{10}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AM}=\dfrac{3}{10}\overrightarrow{AB}+\dfrac{7}{10}\overrightarrow{AC}\)
Lời giải:
Theo đề thì $\overrightarrow{3BM}=7\overrightarrow{MC}=-7\overrightarrow{CM}$
Lại có:
$\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}$
$\Rightarrow 3\overrightarrow{AM}=3\overrightarrow{AB}+3\overrightarrow{BM}=3\overrightarrow{AB}-7\overrightarrow{CM}(1)$
$\overrightarrow{AM}=\overrightarrow{AC}+\overrightarrow{CM}$
$\Rightarrow 7\overrightarrow{AM}=7\overrightarrow{AC}+7\overrightarrow{CM}(2)$
Từ $(1);(2)\Rightarrow 10\overrightarrow{AM}=3\overrightarrow{AB}+7\overrightarrow{AC}$
$\Rightarrow \overrightarrow{AM}=\frac{3}{10}\overrightarrow{AB}+\frac{7}{10}\overrightarrow{AC}$