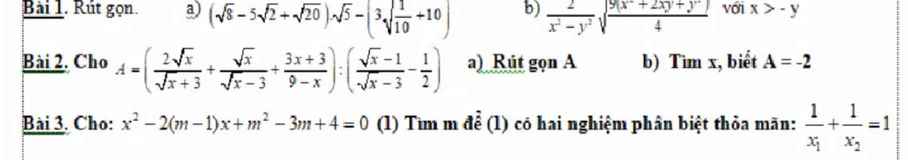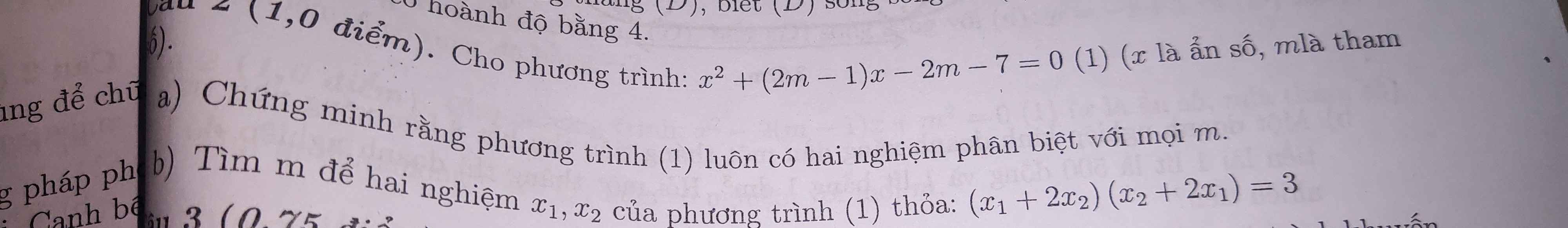\(x^2-2\left(m-2\right)x+m^2+2m-3=0\left(1\right)\)
Để phương trình có hai nghiệm phân biệt thì Δ' > 0
\(\Rightarrow\left(m-2\right)^2-m^2-2m+3>0\Leftrightarrow m^2-4m+4-m^2-2m+3>0\Leftrightarrow-6m+7>0\Leftrightarrow m< \dfrac{7}{6}\)\)
Theo viét : \(\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\\x_1x_2=m^2+2m-3\end{matrix}\right.\)\)
Lại có :\( \dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{5}\)
\(\Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{x_1+x_2}{5}\)
\(\Rightarrow\left(x_1+x_2\right)\left(x_1x_2\right)=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(2m-4\right)\left(m^2+2m-3\right)=5\left(2m-4\right)\)
\(\Leftrightarrow2m^3+4m^2-6m-4m^2-8m+12=10m-20\)
\(\Leftrightarrow2m^3-24m+32=0\) \(\Leftrightarrow\left[{}\begin{matrix}m=-4\left(n\right)\\m=2\left(l\right)\end{matrix}\right.\)
Vậy \(m=-4\) thì thỏa điều kiện





 Mình đang cần rất gấp từ câu 7 đến câu 21. Mọi người giải giúp mình. Mình cảm ơn !
Mình đang cần rất gấp từ câu 7 đến câu 21. Mọi người giải giúp mình. Mình cảm ơn !