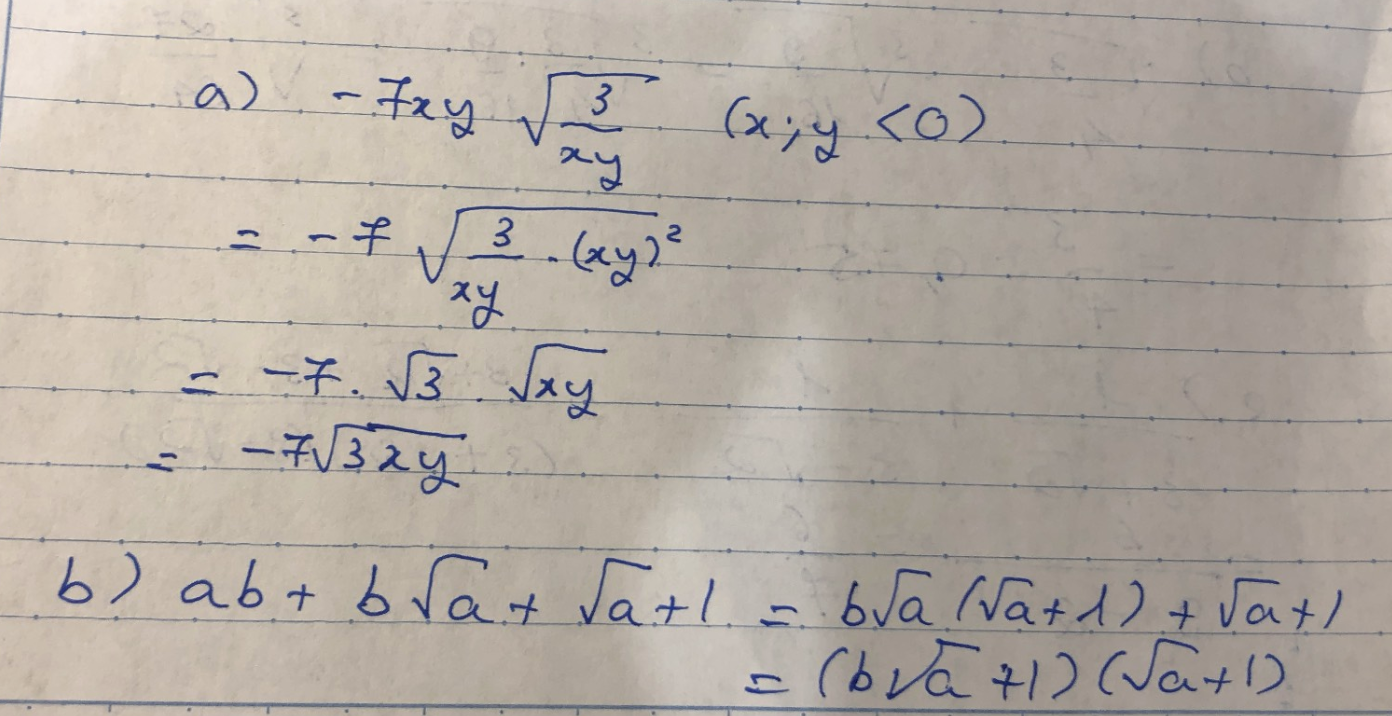a) Ta có: \(-7xy\cdot\sqrt{\dfrac{3}{xy}}\)
\(=\dfrac{-7xy\cdot\sqrt{3xy}}{xy}\)
\(=-7\sqrt{3}\cdot\sqrt{xy}\)
b) Ta có: \(ab+b\sqrt{a}+\sqrt{a}+1\)
\(=b\sqrt{a}\left(\sqrt{a}+1\right)+\left(\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)\left(b\sqrt{a}+1\right)\)
$a)-7xy.\sqrt{\dfrac{3}{xy}}$
$=-7.\sqrt{x^2y^2.\dfrac{3}{xy}}(do \,x,y>0a\to xy>0)$
$=-7.\sqrt{\dfrac{xy}{3}}$
$b)ab+b\sqrt{a}+\sqrt{a}+1(a \ge 0)$
$=b\sqrt{a}(\sqrt{a}+1)+\sqrt{a}+1$
$=(\sqrt{a}+1)(b\sqrt{a}+1)$