Giải:
a, Xét \(\Delta ABD,\Delta ACD\) có:
\(AB=AC\left(gt\right)\)
\(\widehat{BAD}=\widehat{CAD}\left(gt\right)\)
AD: cạnh chung
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{ACD}\) ( góc t/ứng ) ( đpcm )
b, Ta có: AB = AC nên t/g ABC cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Mà \(\widehat{ABD}=\widehat{ACD}\)
\(\Rightarrow\widehat{ABC}-\widehat{ABD}=\widehat{ACB}-\widehat{ACD}\)
\(\Rightarrow\widehat{DBC}=\widehat{DCB}\) ( đpcm )
Vậy...
a) Xét \(\Delta\)ABD và\(\Delta\)ACD có:
AB = AC
góc BAD = CAD
AD :chung
\(\Rightarrow\)\(\Delta\)ABD = \(\Delta\)ACD (1)
b)Từ (1) \(\Rightarrow\)BD = CD
Do đó tam giác BDC cân tại D
Suy ra hai góc DBC = DCB
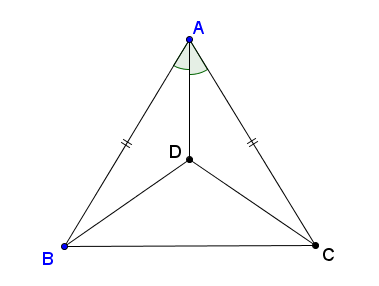


 Cho hình vẽ
Cho hình vẽ