Question

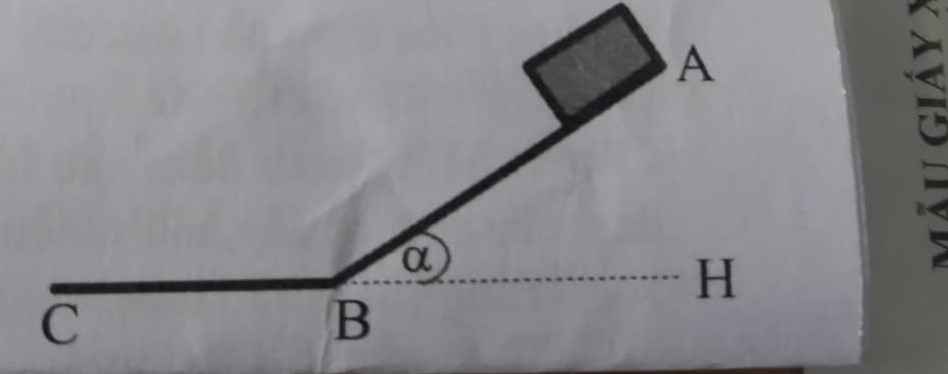
1 vật có m= 5kg trượt không vận tốc đầu từ đỉnh của mặt phẳng nghiêng có chiều cao 20m. α=30^o so với phương ngang, μ=\(\dfrac{\sqrt{3}}{10}\)

a/ Dùng định lí động năng tính v của vật tại chân mặt phẳng nghiêng

b/ Đến chân mặt phẳng nghiêng, vật tiếp tục trượt lên mặt phẳng nằm ngang với ma sát không đổi. Tính s vật đi thêm cho đến lúc dừng

Answer 1

Ta có: \(A=A_{\left(\overrightarrow{Fms}\right)}+A_{\left(\overrightarrow{N}\right)}=F_{ms}s\cos\beta+0\) ( Bổ sung: \(\sin\alpha=\dfrac{h}{S}\Rightarrow S=40\left(m\right)\) )

\(\Rightarrow A=\mu mg\cos\alpha.40.\cos\left(180^0\right)=\dfrac{\sqrt{3}}{10}5.10.\dfrac{\sqrt{3}}{2}.40.\left(-1\right)=-300\left(J\right)\) 

Chọn mốc thế năng tại vị trí chân mặt phẳng nghiêng:

Cơ năng của vật lúc bắt đầu trượt: \(W_1=W_{đ1}+W_{t1}=\dfrac{1}{2}mv_1^2+mgz_1\)

Cơ năng của vật tại chân mặt phẳng nghiêng: \(W_2=\dfrac{1}{2}mv_2^2+mgz_2\) 

Do vật chịu thêm tác dụng của lực ma sát nên cơ năng của vật sẽ không được bảo toàn. Nên công của các lực cản bằng độ biến thiên cơ năng của vật

\(A_{\left(\overrightarrow{Fc}\right)}=\Delta W=W_2-W_1\) 

\(\Rightarrow-300=\left(\dfrac{1}{2}mv_2^2+mgz_2\right)-\left(\dfrac{1}{2}mv_1^2+mgz_1\right)\)

\(\Rightarrow-300=\dfrac{1}{2}mv_2^2-mgz_1\Rightarrow v_2=2\sqrt{170}\left(m/s\right)\)

b) với ma sát không đổi \(\mu=\dfrac{\sqrt{3}}{10}\) ta dễ chứng minh được công thức: \(a=-\mu g=\dfrac{-\sqrt{3}}{10}.10=-\sqrt{3}\)

Ta có hệ thức liên hệ:\(v^2-v_2^2=2aS\Rightarrow S=\dfrac{-v_2^2}{2a}=\dfrac{-\left(2\sqrt{170}\right)^2}{-2\sqrt{3}}=\dfrac{680\sqrt{3}}{6}\left(m\right)\)

Done :D