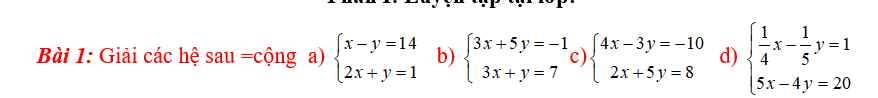a: \(\left\{{}\begin{matrix}x-y=14\\2x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y+2x+y=14+1\\x-y=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=15\\x-y=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=x-14=5-14=-9\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}3x+5y=-1\\3x+y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+5y-3x-y=-1-7\\3x+y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4y=-8\\3x=7-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\3x=7-\left(-2\right)=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}4x-3y=-10\\2x+5y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x-3y=-10\\4x+10y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-3y-4x-10y=-10-16\\4x+10y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-13y=-26\\2x+5y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\2x=8-5y=8-5\cdot2=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}\dfrac{1}{4}x-\dfrac{1}{5}y=1\\5x-4y=20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x-4y=20\\5x-4y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0x=0\\5x-4y=20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in R\\4y=5x-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=\dfrac{5}{4}x-5\end{matrix}\right.\)
\(a,\left\{{}\begin{matrix}x-y=14\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=15\\x-y=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{15}{3}=5\\y=x-14=5-14=-9\end{matrix}\right.\\ Vậy:\left(x;y\right)=\left(5;-9\right)\)
\(b,\left\{{}\begin{matrix}3x+5y=-1\\3x+y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4y=-8\\3x+y=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{8}{4}=-2\\3x+\left(-2\right)=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\x=\dfrac{7+2}{3}=3\end{matrix}\right.\\ Vậy:\left(x;y\right)=\left(3;-2\right)\)
a) \(\left\{{}\begin{matrix}x-y=14\\2x+y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=15\\2x+y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\2x+y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\10+y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-9\end{matrix}\right.\)
Vậy hệ PT có nghiệm duy nhất: \(\left\{{}\begin{matrix}x=5\\y=-9\end{matrix}\right.\)
b)\(\left\{{}\begin{matrix}3x+5y=-1\\\text{3x + y = 7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2\\3x+y=\text{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
Vậy hệ PT có nghiệm duy nhất: \(\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
c)\(\left\{{}\begin{matrix}4x-3y=-10\\2x+5y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x-3y=-10\\4x+10y=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+10y=16\\y=\dfrac{6}{\text{7}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+\dfrac{60}{\text{7}}=16\\y=\dfrac{6}{\text{7}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x=\dfrac{52}{\text{7}}\\y=\dfrac{6}{\text{7}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{52}{28}\\y=\dfrac{6}{\text{7}}\end{matrix}\right.\)'
Vậy hệ PT có nghiệm duy nhất: \(\left\{{}\begin{matrix}x=\dfrac{52}{28}\\y=\dfrac{6}{\text{7}}\end{matrix}\right.\)