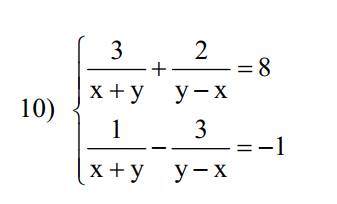Lời giải:
Đặt $\frac{1}{x+y}=a; \frac{1}{y-x}=b$ thì hệ trở thành:
$3a+2b=8$
$a-3b=-1$
$\Rightarrow 3a+2b-3(a-3b)=8-3(-1)$
$\Leftrightarrow 11b=11$
$\Leftrightarrow b=1$
$a=-1+3b=-1+3.1=2$
Vậy: $\frac{1}{x+y}=a=2\Rightarrow x+y=\frac{1}{2}$
$\frac{1}{y-x}=b=1\Rightarrow y-x=1$
$\Rightarrow y=(\frac{1}{2}+1):2=\frac{3}{4}; x=(\frac{1}{2}-1):2=\frac{-1}{4}$