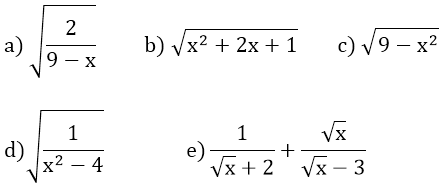a)
Căn thức có nghĩa khi \(9-x>0\Leftrightarrow x< 9\)
b)
\(\sqrt{x^2+2x+1}=\sqrt{\left(x+1\right)^2}\)
Mà \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow\sqrt{\left(x+1\right)^2}\ge0\forall x\)
=> Căn thức \(\sqrt{x^2+2x+1}\) luôn được xác định với mọi giá trị x.
=> \(x\in R\)
c)
Căn thức có nghĩa khi \(9-x^2\ge0\Leftrightarrow x^2\le9\)
\(\Leftrightarrow-3\le x\le3\)
d)
Căn thức có nghĩa khi \(x^2-4>0\Leftrightarrow x^2>4\Leftrightarrow x>2\)
e)
Căn thức có nghĩa khi \(\left\{{}\begin{matrix}\sqrt{x}\ge0\\\sqrt{x}+2\ne0\left(luôn.đúng\right)\\\sqrt{x}-3\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt{x}\ne3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)