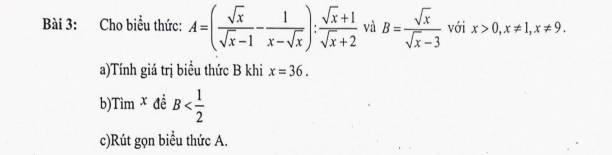a) Thay x=36 vào B ta có:
\(B=\dfrac{\sqrt{36}}{\sqrt{36}-3}=\dfrac{6}{6-3}=2\)
b) \(B< \dfrac{1}{2}\) khi:
\(\dfrac{\sqrt{x}}{\sqrt{x}-3}< \dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}}{2\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}-3}{2\left(\sqrt{x}-3\right)}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
Mà: \(\sqrt{x}+3\ge3>0\forall\left(x\ge0\right)\)
\(\Leftrightarrow2\left(\sqrt{x}-3\right)< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Kết hợp với đk:
\(0< x< 9\)
c) \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(A=\left[\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
\(A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
\(A=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
\(A=\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
a: Khi x=36 thì \(B=\dfrac{6}{6-3}=\dfrac{6}{3}=2\)
b: B<1/2
=>B-1/2<0
=>\(\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{1}{2}< 0\)
=>\(\dfrac{2\sqrt{x}-\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
=>\(\dfrac{\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
=>căn x-3<0
=>0<=x<9
c: \(A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
\(=\dfrac{x-1}{x-1}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}}=\dfrac{\sqrt{x}+2}{\sqrt{x}}\)