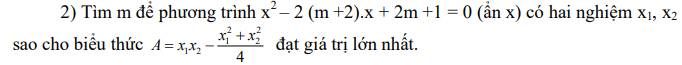\(x^2-2\left(m+2\right)x+2m+1=0\left(1\right)\)
\(\Delta'=\left(m+2\right)^2-2m-1=m^2+4m+4-2m-1=\left(m+1\right)^2+3>0\forall m\)
⇒ Phương trình (1) luôn có hai nghiệm phân biệt
Theo viét :\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+2\right)\\x_1x_2=2m+1\end{matrix}\right.\)
Ta có : \(A=x_1x_2-\dfrac{x_1^2+x_2^2}{4}=x_1x_2-\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{4}\) \(=2m+1-\dfrac{4\left(m+2\right)^2-2\left(2m+1\right)}{4}=2m+1-\dfrac{4m^2+16m+16-4m-2}{4}\) \(2m+1-m^2-4m-4+m+\dfrac{1}{2}=-m^2-m-\dfrac{5}{2}=-\left(m^2+m+\dfrac{5}{2}\right)=-\left(m^2+2.\dfrac{1}{2}m+\dfrac{1}{4}+\dfrac{9}{4}\right)=-\left(m+\dfrac{1}{2}\right)^2-\dfrac{9}{4}\) \(\le-\dfrac{9}{4}\)
Vậy \(A_{max}=-\dfrac{9}{4}\), đạt được khi \(m=-\dfrac{1}{2}\)