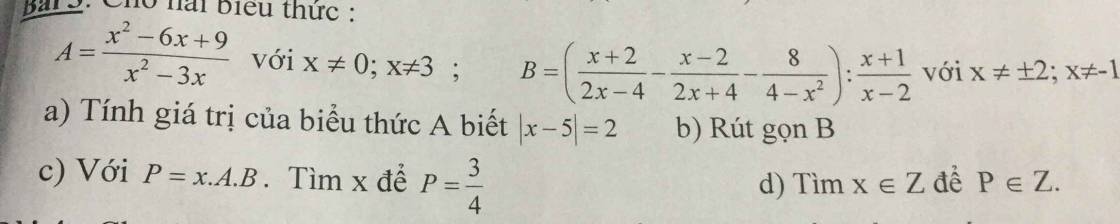`a)` Với `x \ne 0,x \ne 3` có:
`A=[x^2-6x+9]/[x^2-3x]=[(x-3)^2]/[x(x-3)]=[x-3]/x`
Có: `|x-5|=2<=>[(x-5=2),(x-5=-2):}<=>[(x=7(t//m)),(x=3(ko t//m)):}`
Thay `x=7` vào `A` có: `A=[7-3]/7=4/7`
___________________________________________
`b)` Với `x \ne +-2;x \ne -1` có:
`B=([x+2]/[2x-4]-[x-2]/[2x+4]-8/[4-x^2]):[x+1]/[x-2]`
`B=[(x+2)^2-(x-2)^2+16]/[2(x-2)(x+2)].[x-2]/[x+1]`
`B=[(x+2-x+2)(x+2+x-2)+16]/[2(x+2)]. 1/[x+1]`
`B=[4.2x+16]/[2(x+2)(x+1)]`
`B=[8(x+2)]/[2(x+2)(x+1)]`
`B=4/[x+1]`
___________________________________________
`c)` Với `x \ne 0,x \ne 3;x \ne +-2;x \ne -1` có:
`P=3/4<=>x.A.B=3/4`
`<=>x.[x-3]/x. 4/[x+1]=3/4`
`<=>[4x-12]/[x+1]=3/4`
`<=>4(4x-12)=3(x+1)`
`<=>16x-48=3x+3`
`<=>13x=51<=>x=51/13` (t/m)
___________________________________________
`d)` Với `x \ne 0,x \ne 3,x \ne +-2;x \ne -1` có:
`P=[4x-12]/[x+1]=[4x+4-16]/[x+1]=4-16/[x+1]`
`P in ZZ<=>4-16/[x+1] in ZZ`
`=>16/[x+1] in ZZ`
`=>x+1 in Ư_[16]`
Mà `Ư_[16] ={+-1;+-2;+-4;+-8;+-16}`
\begin{array}{|c|c|c|}\hline x+1&-1&1&-2&2&-4&4&-8&8&-16&16\\\hline x& -2&0&-3&1&-5&3&-9&7&-17&15 \\\hline\end{array}
Mà `x in ZZ;x \ne 0;x \ne 3;x \ne +-2;x \ne -1`
`=>x in {-3;1;-5;-9;7;-17;15}`