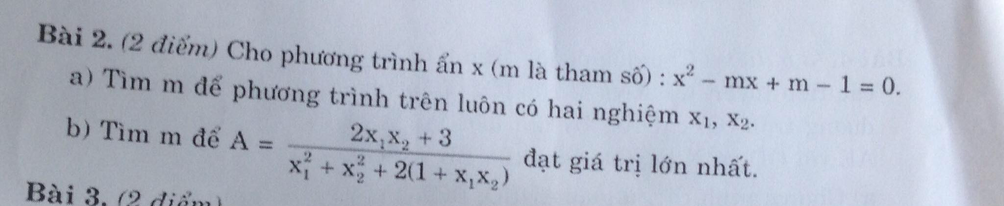\(x^2-mx+m-1=0\)
\(\Delta\ge0\Leftrightarrow m^2-4\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\ge0\left(luôndung\right)\)
\(A=\dfrac{2x1.x2+3}{x1^2+x2^2+2\left(1+x1x2\right)}=\dfrac{2x1x2+3}{\left(x1+x2\right)^2+1}=\dfrac{2\left(m-1\right)+3}{m^2+1}\Leftrightarrow A\left(m^2+1\right)=2\left(m-1\right)+3\Leftrightarrow Am^2+A=2m+1\Leftrightarrow Am^2-2m+A-1=0\left(1\right)\Rightarrow\left[{}\begin{matrix}TH:A=0\Rightarrow\left(1\right)\Leftrightarrow m=-\dfrac{1}{2}\\TH:A\ne0\Rightarrow\Delta'\ge0\Leftrightarrow1-A\left(A-1\right)\ge0\Leftrightarrow\dfrac{1-\sqrt{5}}{2}\le A\le\dfrac{1+\sqrt{5}}{2}\end{matrix}\right.\)
\(\Rightarrow minA=\dfrac{1-\sqrt{5}}{2}\Leftrightarrow m=....\)
\(thayA=\dfrac{1-\sqrt{5}}{2}\) \(vào\left(1\right)\Rightarrow m=....\)