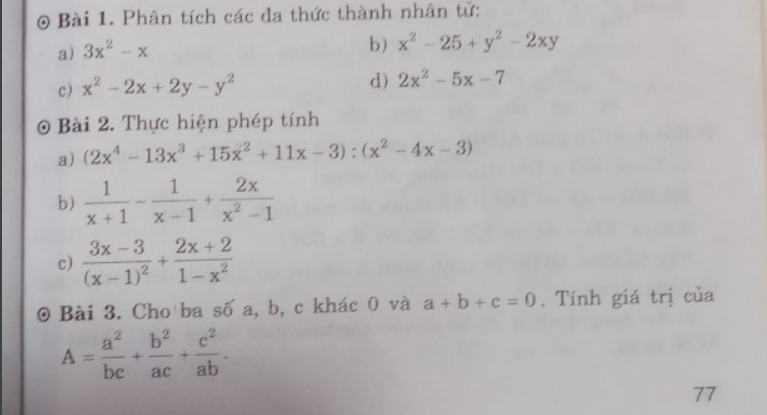Bài 1:
a. $3x^2-x=x(3x-1)$
b. $x^2-25+y^2-2xy=(x^2-2xy+y^2)-25=(x-y)^2-5^2=(x-y-5)(x-y+5)$
c. $x^2-2x+2y-y^2=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)$
$=(x-y)(x+y-2)$
d.
$2x^2-5x-7=(2x^2+2x)-(7x+7)=2x(x+1)-7(x+1)$
$=(x+1)(2x-7)$
Bài 2:
a. $2x^4-13x^3+15x^2+11x-3=2x^2(x^2-4x-3)-5x(x^2-4x-3)+(x^2-4x-3)$
$=(x^2-4x-3)(2x^2-5x+1)$
Vậy $(2x^4-13x^3+15x^2+11x-3): (x^2-4x-3)=2x^2-5x+1$
b.
\(\frac{1}{x+1}-\frac{1}{x-1}+\frac{2x}{x^2-1}=\frac{x-1}{(x+1)(x-1)}-\frac{x+1}{(x-1)(x+1)}+\frac{2x}{(x-1)(x+1)}\)
\(=\frac{x-1-(x+1)+2x}{(x-1)(x+1)}=\frac{2x-2}{(x+1)(x-1)}=\frac{2(x-1)}{(x+1)(x-1)}=\frac{2}{x+1}\)
c.
\(=\frac{3(x-1)}{(x-1)^2}-\frac{2(x+1)}{(x-1)(x+1)}=\frac{3}{x-1}-\frac{2}{x-1}=\frac{1}{x-1}\)
Bài 3:
\(A=\frac{a^3}{abc}+\frac{b^3}{abc}+\frac{c^3}{abc}=\frac{a^3+b^3+c^3}{abc}=\frac{(a+b)^3-3ab(a+b)+c^3}{abc}\)
\(=\frac{(-c)^3-3ab(-c)+c^3}{abc}=\frac{-c^3+3abc+c^3}{abc}=\frac{3abc}{abc}=3\)
Bài 1 a. 3x2−x=x(3x−1)3x2−x=x(3x−1)
b.x2−25+y2−2xy=(x2−2xy+y2)−25=(x−y)2−52=(x−y−5)(x−y+5)x2−25+y2−2xy=(x2−2xy+y2)−25=(x−y)2−52=(x−y−5)(x−y+5)
c. x2−2x+2y−y2=(x2−y2)−(2x−2y)=(x−y)(x+y)−2(x−y)x2−2x+2y−y2=(x2−y2)−(2x−2y)=(x−y)(x+y)−2(x−y)=(x−y)(x+y−2)=(x−y)(x+y−2)
d.2x2−5x−7=(2x2+2x)−(7x+7)=2x(x+1)−7(x+1)2x2−5x−7=(2x2+2x)−(7x+7)=2x(x+1)−7(x+1)=(x+1)(2x−7)
Bài 2: a.2x4−13x3+15x2+11x−3=2x2(x2−4x−3)−5x(x2−4x−3)+(x2−4x−3)2x4−13x3+15x2+11x−3=2x2(x2−4x−3)−5x(x2−4x−3)+(x2−4x−3)=(x2−4x−3)(2x2−5x+1)=(x2−4x−3)(2x2−5x+1)
Vậy (2x4−13x3+15x2+11x−3):(x2−4x−3)=2x2−5x+1(2x4−13x3+15x2+11x−3):(x2−4x−3)=2x2−5x+1
b.1x+1−1x−1+2xx2−1=x−1(x+1)(x−1)−x+1(x−1)(x+1)+2x(x−1)(x+1)1x+1−1x−1+2xx2−1=x−1(x+1)(x−1)−x+1(x−1)(x+1)+2x(x−1)(x+1)=x−1−(x+1)+2x(x−1)(x+1)=2x−2(x+1)(x−1)=2(x−1)(x+1)(x−1)=2x+1=x−1−(x+1)+2x(x−1)(x+1)=2x−2(x+1)(x−1)=2(x−1)(x+1)(x−1)=2x+1
c.=3(x−1)(x−1)2−2(x+1)(x−1)(x+1)=3x−1−2x−1=1x−1
Bài 4:
a. Tứ giác $ADME$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên $ADME$ là hình chữ nhật.
b.
Vì $ADME$ là hcn nên $DM\parallel AE$ và $DM=AE(*)$
Do $K,M$ đối xứng nhau qua $D$ nên $K, D, M$ thẳng hàng và $KD=DM (**)$
Từ $(*); (**)\Rightarrow KD\parallel AE$ và $KD=AE$ nên $KDEA$ là hbh.
c.
Xét tam giác $BAH$ và $ACH$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{BAH}=\widehat{ACH}$ (cùng phụ $\widehat{B}$)
$\Rightarrow \triangle BAH\sim \triangle ACH$ (g.g)
$\Rightarrow \frac{BH}{AH}=\frac{AH}{CH}\Rightarrow BH.CH=AH^2$ (đpcm)
d. Xét tam giác $AHC$ và $MEC$ có:
$\widehat{C}$ chung
$\widehat{AHC}=\widehat{MEC}=90^0$
$\Rightarrow \triangle AHC\sim \triangle MEC$ (g.g)
$\Rightarrow \frac{AH}{ME}=\frac{HC}{EC}$ hay $\frac{AH}{AD}=\frac{HC}{EC}$
Xét tam giác $AHD$ và $CHE$ có:
$\widehat{A_1}=\widehat{C_1}$ (cùng phụ $\widehat{B}$)
$\frac{AH}{AD}=\frac{CH}{CE}$ (cmt)
$\Rightarrow \triangle AHD\sim \triangle CHE$ (c.g.c)
$\Rightarrow \widehat{H_1}=\widehat{H_2}$
$\Rightarrow \widehat{H_1}+\widehat{AHE}=\widehat{H_2}+\widehat{AHE}$
Hay $\widehat{DHE}=\widehat{AHM}=90^0$
$\Rightarrow DHE$ là tam giác vuông tại $H$