Ôn tập toán 7

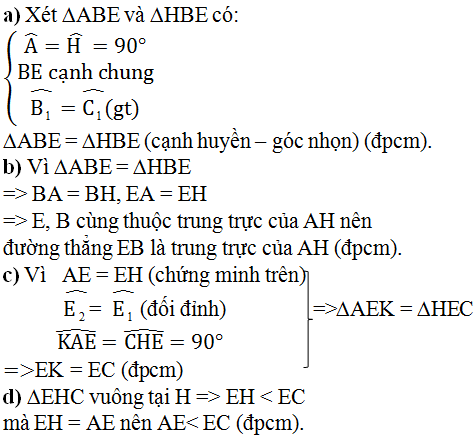
Cho tam giác ABC vuông tại A; đường phân giác BE. Kẻ EH vuông góc với BC \(\left(H\in BC\right)\). Gọi K là giao điểm của AB vag HE. Chứng minh rằng :

a) \(\Delta ABE=\Delta HBE\)

b) BE là đường trung trực của đoạn thẳng AH

c) EK = EC

d) AE < EC

Chứng minh rằng : Nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại A

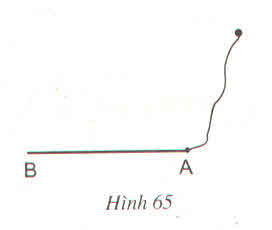
Ứng dụng : Một tờ giấy bị rách ở mép (h.65). Hãy dùng thước và compa dựng đường vuông góc với cạnh AB tại A

Cho hình 66.

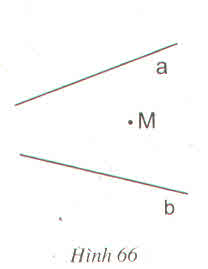
Không vẽ giao điểm của a, b hãy nêu cách vẽ đường thẳng đi qua giao điểm này và điểm M ?

Đố :

Cho tam giác ABC. Em hãy tô mầu để xác định phần bên trong của tam giác gồm các điểm M sao cho :

                         MA < MB < MC

(Hướng dẫn: Trước tiên tô màu để xác định các điểm M ở trong tam giác mà MA < MB lần thứ hai là MB < MC. Phần trong tam giác được tô mầu hai lần là phải tìm)