Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Khi đó
A.\(AM = 2GM\). B.\(AM = 2AG\). C.\(GA = 3GM\). D.\(GA = 2GM\).
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Khi đó
A.\(AM = 2GM\). B.\(AM = 2AG\). C.\(GA = 3GM\). D.\(GA = 2GM\).
Cho tam giác ABC cân tại A có \(\widehat {BAC} = 40^\circ \). Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Khi đó
A.\(OA = OB = AB\). B.\(OA = OB = OC\). C.\(OB = OC = BC\). D.\(OC = OA = AC\).
Đáp án: B. \(OA = OB = OC\).
Trả lời bởi Hà Quang MinhCho tam giác ABC có BC > AC, I là giao điểm của hai đường phân giác góc A và góc B. Khi đó
A.\(\widehat {ICA} = \widehat {ICB}\). B.\(\widehat {IAC} = \widehat {IBC}\). C.\(\widehat {ICA} > \widehat {ICB}\). D.\(\widehat {ICA} < \widehat {IBC}\).
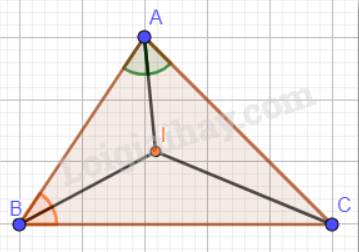
Ta có: I là giao điểm của hai đường phân giác góc A và góc B nên suy ra: CI là đường phân giác của góc C.
Vậy \(\widehat {ICA} = \widehat {ICB}\) ( tính chất tia phân giác của một góc).
Đáp án: A. \(\widehat {ICA} = \widehat {ICB}\).
Trả lời bởi Kiều Sơn TùngCho tam giác nhọn ABC có AB < AC. Hai đường cao AD và CE cắt nhau tại H. Khi đó
A.\(\widehat {HAB} = \widehat {HAC}\).
B.\(\widehat {HAB} > \widehat {HAC}\).
C.\(\widehat {HAB} = \widehat {HCB}\).
D.\(\widehat {HAC} = \widehat {BAC}\).
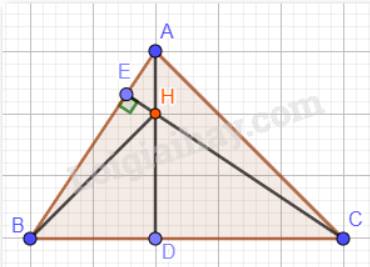
Ta có: AB < AC nên \(\widehat {ACB} < \widehat {ABC}\) (góc ACB đối diện với cạnh AB; góc ABC đối diện với cạnh AC)
Mà tam giác ADB và tam giác ADC vuông tại D.
Vì tổng hai góc nhọn trong một tam giác vuông bằng 90°.
Mà \(\widehat {ACB} < \widehat {ABC}\).
Suy ra: \(90^\circ - \widehat {ACB} > 90^0 - \widehat {ABC}\) hay \(\widehat {DAC} > \widehat {DAB}\).
Vậy \(\widehat {HAC} > \widehat {HAB}\) hay \(\widehat {HAB} < \widehat {HAC}\).
Suy ra: A, B, D sai.
Đáp án: C.\(\widehat {HAB} = \widehat {HCB}\).
Trả lời bởi Kiều Sơn Tùng
Đáp án: D. \(GA = 2GM\).
Trả lời bởi Kiều Sơn Tùng