Có hai xã cùng ở một bên bờ sông Lam. Người ta đo được khoảng cách từ trung tâm A, B của hai xã đó đến bờ sông lần lượt là AA 500 m, BB 600 m và AB 2 200 m (Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn AB sao cho tổng khoảng cách từ hai vị trí A, B đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
Đọc tiếp
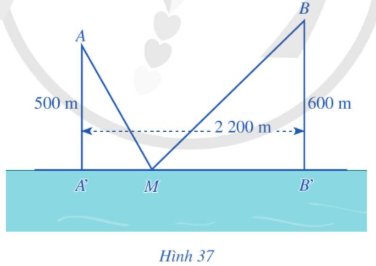
Có hai xã cùng ở một bên bờ sông Lam. Người ta đo được khoảng cách từ trung tâm A, B của hai xã đó đến bờ sông lần lượt là AA' = 500 m, BB' = 600 m và A'B' = 2 200 m (Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A'B' sao cho tổng khoảng cách từ hai vị trí A, B đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
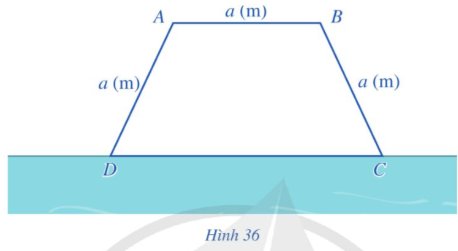

Gọi độ dài của hàng rào song sông với bờ sông là x(m) với x>0
Gọi độ dài của mỗi hàng rào trong ba hàng rào song song nhau là y(m) với y>0
Diện tích đất mà bác nông dân rào được là: \(xy\left( {{m^2}} \right)\)
Tổng chi phí là 15.000.000 đồng nên ta có phương trình:
\(x*60000 + 3y*50000 = 15000000 = > 6x + 15y = 1500\)
Áp dụng bất đẳng thức Cauchy cho hai số dương ta có:
\(6x + 15y \ge 2\sqrt {6x.5y} = > 1500 \ge 2\sqrt {90xy} = > xy \le 6250\)
Vậy diện tích lớn nhất mà bác nông dân có thể tạo rào là 6250\(\left( {{m^2}} \right)\)
Trả lời bởi datcoder