Hãy nêu những cách xác định mặt phẳng, kí hiệu mặt phẳng ?
Bài 6: Ôn tập chương Đường thẳng và mặt phẳng trong không gian. Quan hệ song song.
SK
Hướng dẫn giải
Thảo luận (1)
SK
Thế nào là đường thẳng song song với đường thẳng ? Đường thẳng song song với mặt phẳng ? Mặt phẳng song song với mặt phẳng ?
Hướng dẫn giải
Thảo luận (1)
- Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung.
- Một đường thẳng và một mặt phẳng gọi là song song với nhau nếu chúng không có điểm chung.
- Hai mặt phẳng gọi là song song nếu chúng không có điểm chung.
SK
Nêu phương pháp chứng minh 3 điểm thẳng hàng ?
Hướng dẫn giải
Thảo luận (2)
Muốn chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó là các điểm chung của hai mặt phẳng phân biệt. Khi đó chúng sẽ thẳng hàng trên giao tuyến của hai mặt phẳng đó
Trả lời bởi Trương Hồng Hạnh
SK
Nêu phương pháp chứng minh 3 đường thẳng đồng quy ?
Hướng dẫn giải
Thảo luận (1)
Muốn chứng minh ba đường thẳng đồng quy ta chứng minh giao điểm của hai đường này là điểm chung của hai mặt phẳng mà giao tuyến là đường thứ ba
Trả lời bởi Trương Hồng Hạnh
SK
Nêu phương pháp chứng minh :
- Đường thẳng song song với đường thẳng
- Đường thẳng song song với mặt phẳng
- Mặt phẳng song song với mặt phẳng
Hướng dẫn giải
Thảo luận (1)
Muốn chứng minh đường thẳng a // (P), ta chứng minh đường thẳng a song song với đường thẳng b mà đường thẳng b song song với mặt phẳng (P) (a và (P) không có điểm chung)
Trả lời bởi qwerty
SK
Phát biểu định lí Ta - lét trong không gian ?
Hướng dẫn giải
Thảo luận (1)
Ba mặt phẳng đôi một song song chắn ra trên hai cát tuyến bất kì hai đoạn thẳng tỉ lệ .
Trả lời bởi _silverlining
SK
Nêu cách xác định thiết diện tạo bởi một mặt phẳng với một hình chóp, hình hộp, hình lăng trụ ?
Hướng dẫn giải
Thảo luận (1)
Xác định thiết diện của hình chóp,hình lăng trụ dựa trên quan hệ vuông góc thường dựa trên các nguyên tắc sau: *Mặt phẳng chứa thiết diện qua một điểm và vuông góc với một đường thẳng thì chứa hai đường thẳng cắt nhau vuông góc với đường thẳng đó. * Mặt phẳng chứa thiết diện qua một đường thẳng và vuông góc với một mặt phẳng thì chứa một đường thẳng vuông góc với mặt phẳng đó.
Trả lời bởi Quang Duy
SK
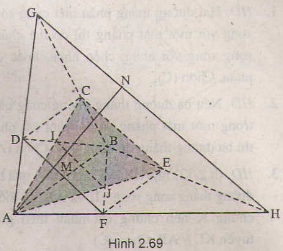
Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng :
a) Tìm giao tuyến của các mặt phẳng sau :
(AEC) và (BFD); (BCE) và (ADF)
b) Lấy M là điểm thuộc đoạn DF. Tìm giao điểm của đường thẳng AM với mặt phẳng (BCE)
c) Chứng minh hai đường thẳng AC và BF không cắt nhau
Hướng dẫn giải
Thảo luận (1)
a) Trong (ABCD) : AC ∩ BD = I, Trong ( ABEF): AE ∩ BF = J
=> (ACE) ∩ (BDF) = IJ
Tương tự (BCE) ∩ ( ADF) = GH
b) Trong (AGH): AM ∩ GH = N, chứng minh N AM và N
(BCE)
c) Chứng minh bằng phương pháp phản chứng. Giả sử AC và BE cùng nằm trong một mặt phẳng, lập luận dẫn tới (ABCD) ≡ (ABEF), trái với giả thiết
SK
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P theo thứ tự là trung điểm của các đoạn SA, BC CD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP)
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, hãy tìm giao điểm của đường thẳng SO với mặt phẳng (MNP)
Hướng dẫn giải
Thảo luận (1)
a) Trong mặt phẳng (ABCD) đường thẳng NP cắt đường thẳng AB, AD lần lượt tại E, F. Từ đó có thiết dện là MQPNR.
b) Trong (SAC): SO ∩ MC = K, chứng minh đó là điểm cần tìm
SK
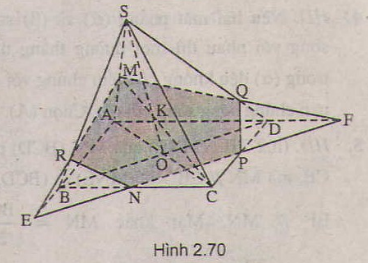
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC) ?
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN) ?
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN) ?
Hướng dẫn giải
Thảo luận (1)
a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
Trả lời bởi _silverlining
- Qua ba điểm không thẳng hàng xác định một mặt phẳng duy nhất. Mặt phẳng đi qua ba điểm không thẳng hàng A, B, C được kí hiệu là mp(ABC) hay (ABC)
- Qua một đường thẳng và một điểm không thuộc đường thẳng đó xác định một mặt phẳng duy nhất. Mặt phẳng đi qua A và đường thẳng d không chứa A được kí hiệu là mp(A;d)
- Qua hai đường thẳng cắt nhau xác định một mặt phẳng duy nhất. Mặt phẳng qua hai đường thẳng cắt nhau a,b được kí hiệu là mp(a;b)
Trả lời bởi Quang Duy