Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm
a) Tính khoảng cách từ tâm O đến dây AB
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB
Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng :
a) EH = EK
b) EA = EC
a)Vì HA=HB nên OH⊥AB
Vì KC=KD nên OK⊥CD
Mặt khác, AB=CD nên OH=OK (hai dây bằng nhau thì cách đều tâm).
ΔHOE=ΔKOE (cạnh huyền, cạnh góc vuông)
Suy ra EH=EK. (1)
b) Ta có AH=KC (một nửa của hai dây bằng nhau). (2)
Từ (1) và (2) suy ra EH+HA=EK+KC hay EA=EC.
Cho đường tròn tâm O bán kính 25cm, dây AB bằng 40 cm. Vẽ dây CD song song với AB và có khoảng cách đến AB bằng 22 cm. Tính độ dài dây CD
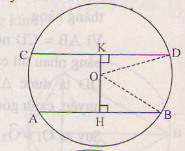
Vẽ , đường thẳng OH cắt CD tại K. Hãy chứng minh
KC=KD và AH=HB.
Tính được OH=15, suy ra OK=7.
Từ đó suy ra KD=24, suy ra CD=48.
Trả lời bởi Khùng ĐiênCho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
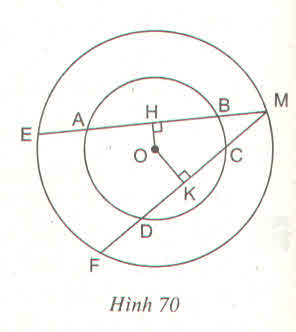
Hãy so sánh các độ dài :
a) OH và OK
b) ME và MF
c) MH và MK
a) Xét đường tròn nhỏ ta được .
b) Xét đường tròn lớn ta được .
c) Từ kết quả câu b) suy ra .
Trả lời bởi Khùng ĐiênCho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF ?
Vẽ OH⊥EFOH⊥EF.
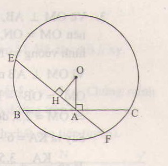
Xét tam giác HOA vuông tại H ta có OH<OA
Suy ra EF>BC..
Nhận xét. Trong các dây đi qua một điểm A ở trong đường tròn, dây vuông góc với OA là dây ngắn nhất.
Cho hình 74 trong đó MN = PQ.
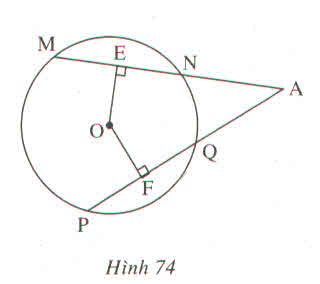
Chứng minh rằng:
a) AE = AF
b) AN = AQ
Cho đường tròn (O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thnawgr AB, CD nằm ngoài đường tròn. Đường tròn (O; OK) cắt KA và KC tại M và N
Chứng minh rằng KM < KN
Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Chứng minh rằng dây AB vuông góc với OI tại I ngắn hơn mọi dây khác đi qua I ?
Tam giác ABC nội tiếp đường tròn (O) có \(\widehat{A}>\widehat{B}>\widehat{C}\). Gọi OH, OI, OK theo thứ tự là khoảng cách từ O đến BC, AC, AB. So sánh các độ dài OH, OI, OK ?
Ta có \(\widehat{A}>\widehat{B}>\widehat{C}\) nên \(BC>AC>AB\)
Do đó \(OH< OI< OK\)
Trả lời bởi Nguyen Thuy HoaCho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng:
a) IO là tia phân giác của một trong hai góc tạo bởi hai dây AB và CD
b) Điểm I chia AB, CD thành các đoạn thẳng bằng nhau đôi một
a) Vẽ OH⊥ABOH⊥AB, ta có HA=HB=4cm.
Xét tam giác HOB vuông tại H, có:
OH2=OB2−HB2=52−42=9⇒OH=3(cm)OH2=OB2−HB2=52−42=9⇒OH=3(cm).
b) Vẽ OK⊥CDOK⊥CD. TỨ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra OK=HI. Ta có HI=4-1=3cm, suy ra OK=3cm.
Vậy OH=OK=3cm.
Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
Trả lời bởi Khùng Điên