Bài 3. Hằng đẳng thức đáng nhớ

a) \(9{{\rm{x}}^2} - 16 = {\left( {3{\rm{x}}} \right)^2} - {4^2} = \left( {3{\rm{x}} - 4} \right)\left( {3{\rm{x}} + 4} \right)\) 

b)  \(25 - 16{y^2} = {5^2} - {\left( {4y} \right)^2} = \left( {5 - 4y} \right)\left( {5 + 4y} \right)\)

\(a)\left( {a - 3b} \right)\left( {a + 3b} \right) = {a^2} - {\left( {3b} \right)^2} = {a^2} - 9{b^2}\)

\(b)\left( {2{\rm{x}} + 5} \right)\left( {2{\rm{x}} - 5} \right) = {\left( {2{\rm{x}}} \right)^2} - {5^2} = 4{{\rm{x}}^2} - 25\)

\(c)\left( {4y - 1} \right)\left( {4y + 1} \right) = {\left( {4y} \right)^2} - {1^2} = 16{y^2} - 1\)

\(a){\left( {x + \dfrac{1}{2}} \right)^2} = {x^2} + 2.x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = {x^2} + x + \dfrac{1}{4}\)

\(b){\left( {2{\rm{x}} + y} \right)^2} = {\left( {2{\rm{x}}} \right)^2} + 2.2{\rm{x}}.y + {y^2} = 4{{\rm{x}}^2} + 4{\rm{x}}y + {y^2}\)

\(c){\left( {3 - x} \right)^2} = {3^2} - 2.3.x + {x^2} = 9 - 6{\rm{x}} + {x^2}\)

\(d){\left( {x - 4y} \right)^2} = {x^2} - 2.x.4y + {\left( {4y} \right)^2} = {x^2} - 8{\rm{x}}y + 16{y^2}\)

\(\left( {a - b} \right)\left( {a + b} \right) = a.a + a.b - ba - b.b = {a^2} - {b^2}\)

a) \({y^2} + y + \dfrac{1}{4} = {y^2} - 2.y.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = {\left( {y - \dfrac{1}{2}} \right)^2}\)

b) \({y^2} + 49 - 14y = {y^2} - 14y + 49 = {y^2} - 2.y.7 + {7^2} = {\left( {y - 7} \right)^2}\)

a) 

Cách 1: Diện tích hình vuông MNPQ là: \({a^2} + ab + ab + {b^2} = {a^2} + 2{\rm{a}}b + {b^2}\)

Cách 2: Độ dài cạnh của hình vuông MNPQ là: \(a + b\)

Diện tích của hình vuông MNPQ là: \(\left( {a + b} \right).\left( {a + b} \right) = {\left( {a + b} \right)^2}\)

b) \(\left( {a + b} \right)\left( {a + b} \right) = a.a + ab + ab + b.b = {a^2} + 2{\rm{a}}b + {b^2}\)     

c)  \(\left( {a - b} \right)\left( {a - b} \right) = a.a - a.b - a.b - b.\left( { - b} \right) = {a^2} - 2{\rm{a}}b + {b^2}\)            

a) * Thay x = 1; y = -1 vào biểu thức P ta được:

\(P = 2.\left[ {1 + \left( { - 1} \right)} \right] = 0\)

Thay x = 1; y = -1 vào biểu thức Q ta được:

\(Q = 2.1 + 2.\left( { - 1} \right) = 0\)

\(\Rightarrow\) Tại x = 1; y = -1, P = Q.

b) * Thay x = 2; y = 3 vào biểu thức P ta được:

\(P = 2.\left( {2 + 3} \right) = 10\)

* Thay x = 2; y = 3 vào biểu thức Q ta được:

\(Q = 2.2 + 2.3 = 10\)

\(\Rightarrow\) Tại x = 2; y = 3, P = Q.

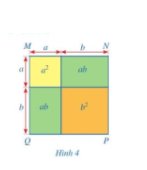
Cách 1: Diện tích hình vuông MNPQ là: \({a^2} + ab + ab + {b^2} = {a^2} + 2{\rm{a}}b + {b^2}\)

Cách 2: Độ dài cạnh của hình vuông MNPQ là: \(a + b\)

Diện tích của hình vuông MNPQ là: \(\left( {a + b} \right).\left( {a + b} \right) = {\left( {a + b} \right)^2}\)

Ta có: \(\begin{array}{l}x\left( {x{y^2} + y} \right) - y\left( {{x^2}y + x} \right)\\ = x.x{y^2} + xy - y.{x^2}y - {\rm{yx}}\\ = {x^2}{y^2} + xy - {x^2}{y^2} - xy = \left( {{x^2}{y^2} - {x^2}{y^2}} \right) + \left( {xy - xy} \right) = 0\end{array}\)

Vậy \(x\left( {x{y^2} + y} \right) - y\left( {{x^2}y + x} \right) = 0\) (đpcm)

Ta có: \({49^2} = {\left( {50 - 1} \right)^2} = {50^2} - 2.50.1 + {1^2} = 2500 - 100 - 1 = 2401\)

Vậy: \({49^2} = 2401\)