Cho tam giác \(ABC\) nhọn. Gọi \(M,N,P\) lần lượt là trung điểm của \(AB;AC;BC\). Kẻ đường cao \(AH\). Chứng minh rằng tứ giác \(MNPH\) là hình thang cân.
Bài 2. Đường trung bình của tam giác
QL
Hướng dẫn giải
Thảo luận (1)
QL
Một mái nhà được vẽ như Hình 13. Tính độ dài \(x\) trong hình mái nhà.
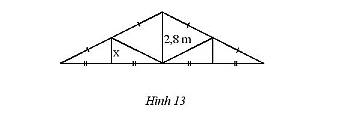
Hướng dẫn giải
Thảo luận (2)
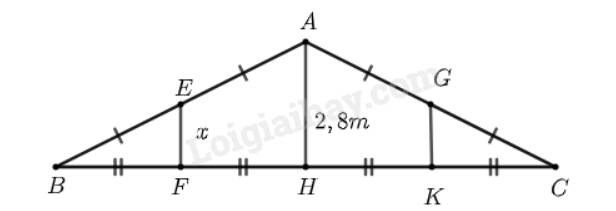
Theo hình vẽ ta có:
\(BE = EA \Rightarrow E\) là trung điểm của \(AB\);
\(BF = FH \Rightarrow F\) là trung điểm của \(BH\).
Vì \(E\)là trung điểm của \(AB\); \(F\)là trung điểm của \(BH\) nên \(EF\) là đường trung bình của tam giác \(ABH\).
\( \Rightarrow EF = \frac{1}{2}AH\) (tính chất đường trung bình)
\( \Leftrightarrow EF = \frac{1}{2}.2,8 = 1,4\).
Vậy \(x = 1,4m\).
Trả lời bởi Kiều Sơn Tùng
QL
Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh \(DE\), cho biết \(BC = 232m\) và \(B,C\) lần lượt là trung điểm của \(AD\) và \(AE\).
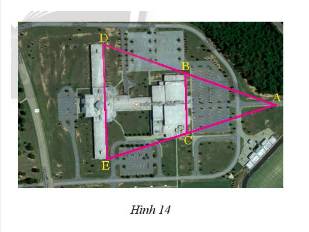
Hướng dẫn giải
Thảo luận (2)
Xét ΔADE có B,C lần lượt là trung điểm của AD,AE
=>BC là đường trung bình
=>DE=2*BC=464(m)
Trả lời bởi Nguyễn Lê Phước Thịnh
- Vì \(M\) là trung điểm của \(AB;N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\). Do đó, \(MN//BC\) (tính chất đường trung bình).
\( \Rightarrow MN//HP\left( {H;P \in BC} \right)\)
Xét tứ giác \(MNPH\) có: \(MN//HP \Rightarrow \) tứ giác \(MNPH\) là hình thang.
- Vì \(M\) là trung điểm của \(AB;P\) là trung điểm của \(AC\) nên \(MP\) là đường trung bình của tam giác \(ABC\). Do đó, \(MP = \frac{1}{2}AC\) (tính chất đường trung bình) (1).
- Xét tam giác \(AHC\) vuông tại \(H\) có:
\(N\)là trung điểm của \(AC\) nên \(HN = \frac{1}{2}AC\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (2).
Từ (1) và (2) suy ra \(MP = HN\).
Xét hình thang \(MNPH\) có: \(MP = HN\) (chứng minh trên).
Do đó, hình thang \(MNPH\) là hình thang cân (dấu hiệu nhận biết hình thang cân).
Trả lời bởi Kiều Sơn Tùng