Bài 12: Dấu hiệu chia hết cho 3, cho 9

a) 537

b) 3471; 9471

a, Chia hết cho ba: 1002

b, chia hết cho 9: 1008

- Số 1546 có tổng 1 + 5 + 4 + 6 = 16. Tổng này chia cho 9 dư 7, chia cho 3 dư 1.

Do đó, số 1546 chia cho 9 dư 7, chia cho 3 dư 1.

- Số 1527 có tổng 1 + 5 + 2 + 7 = 15. Tổng này chia cho 9 dư 6, và chia hết cho 3.

Do đó, số 1527 chia cho 9 dư 6, và chia hết cho 3.

- Số 2468 có tổng 2 + 4 + 6 + 8 = 20. Tổng này chia cho 9 dư 2, chia cho 3 dư 2.

Do đó, số 2468 chia cho 9 dư 2, chia cho 3 dư 2.

- Số 10¹¹ có tổng 1 + 0 + ... + 0 = 1. Tổng này chia cho 9 dư 1, chia cho 3 dư 1.

Do đó, số 10¹¹ chia cho 9 dư 1, chia cho 3 dư 1.

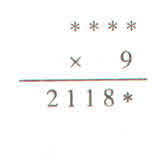
\(\overline{abcd}.9=\overline{2118e}\)

\(\Leftrightarrow\overline{2118e}:9=\overline{abcd}\)

Ta có: 2+1+1+8=12 => \(e=6\)

Xét e=6, ta có: 21186 : 9 = 2354 (nhận)

Vậy a=2; b=3; c=5; d=4; e=6.

a)

\(\overline{5\circledast8}⋮3khi\left(5+\circledast+8\right)⋮3\Rightarrow\left(13+\circledast\right)⋮3\)

\(\Rightarrow\circledast\) = 2 hoặc \(\circledast\) = 5 hoặc \(\circledast\) = 8.

Vậy chữ số thay cho \(\circledast\) là 2 hoặc 5 hoặc 8.

b)

\(\overline{6\circledast3}⋮9khi\left(6+3+\circledast\right)⋮9\Rightarrow\left(9+\circledast\right)⋮9\)

\(\Rightarrow\circledast\) = 0 hoặc \(\circledast\) = 9.

Vậy chữ số thay \(\circledast\) là 0 hoặc 9

c)

\(\overline{43\circledast}⋮3khi\left(4+3+\circledast\right)⋮3\Rightarrow\circledast=2\text{hoặc}\circledast=5\text{hoặc}\circledast=8\left(1\right)\)

\(\overline{43\circledast}⋮5khi\circledast=0\text{hoặc}\circledast5\)

Vì \(\circledast\) phải thỏa mãn (1) và ( 2) nên \(\circledast\) = 5.

d)

Vì \(\overline{\circledast81\circledast}⋮5\) nên dấu \(\circledast\) ở hàng đơn vị phải bằng 0 hoặc 5

Mà \(\overline{\circledast81\circledast}⋮2\) nên dấu \(\circledast\) ở hàng đơn vị phải bằng 0 ( vì 5 là số lẻ ) . Thay vào ta được số : \(\overline{\circledast810}\)

Để \(\overline{\circledast810}⋮9\) thì \(\left(\circledast+8+1+0\right)⋮9=\left(\circledast+9\right)\Rightarrow\circledast=0\text{hoặc}\circledast=9\)

Mà \(\circledast\) lại là số ở hàng nghìn (là số đầu tiên) nên \(\circledast\) ≠ 0. Do đó \(\circledast\) = 9

Vậy ta được số 9810

- Với a = 16 có tổng 1 + 6 = 7. Tổng này chia cho 9 dư 7 nên số này chia cho 9 dư 7. Do đó m = 7.

- Với a = 213 có tổng 2 + 1 + 3 = 6. Tổng này chia cho 9 dư 6 nên số này chia cho 9 dư 6. Do đó m = 6.

- Với a = 827 có tổng 8 + 2 + 7 = 17. Tổng này chia cho 9 dư 8 nên số này chia cho 9 dư 8. Do đó m = 8.

- Với a = 468 có tổng 4 + 6 + 8 = 18. Tổng này chia hết cho 9 (dư 0) nên số này chia hết cho 9. Do đó m = 0.

Số 1347, 6534, 93258 chia hết cho 3

Số 93258 ,6534 chia hết cho 9

Bài giải:

HD: Có thể tính tổng (hiệu) rồi xét xem kết quả tìm được có chia hết cho 3, cho 9 không. Cũng có thể xét xem từng số hạng của tổng (hiệu) có chia hết cho 3, cho 9 không. Chẳng han: 1251 chia hết cho 3 và cho 9, 5316 chỉ chia hết cho 3 mà không chia hết cho 9. Do đó tổng 1251 + 5316 chia hết cho 3 mà không chia hết cho 9.

Đáp số:

a) 1251 + 5316 chia hết cho 3 mà không chia hết cho 9.

b) 5436 - 1324 không chia hết cho 3, không chia hết cho 9.

c) Vì 1 . 2 . 3 . 4 . 5 . 6 = 1 . 2 . 3 . 4 . 5 . 3 . 2 = 9 . 1 . 2 . 4 . 5 . 2 chia hết cho 9 và 27 cũng chia hết cho 9 nên 1 . 2 . 3 . 4 . 5 . 6 + 27 chia hết cho 9. Do đó cũng chia hết cho 3.

Bài làm :

a) \(10^{12}-1\)

Ta có công thức : \(10^n=10000....0\)

Từ công thức ta suy ra : \(10^{12}-1\)  gồm 12 chữ số 9 .

Vì \(99...99\) có tổng các chữ số chia hết cho 9 nên \(10^{12}-1\) chia hết cho 9 và do đó cũng chia hết cho 3. 

b) Từ công thức trên ta suy ra :
\(10^{10}+2=10...02\) .
Số \(10...02\) có tổng các chữ số là \(1+2+0+...=3\) nên \(10...02\) chia hết cho 3 nhưng không chia hết cho 9.
Vậy \(10^{10}+2\) chia hết cho 3 nhưng không chia hết cho 9.