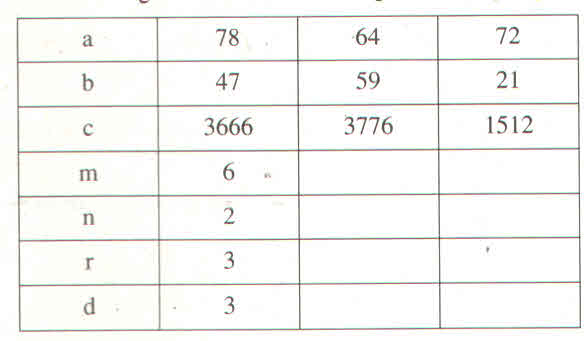
Trong phép nhân \(a.b=c\) gọi :
m là số dư của a khi chia cho 9, n là số dư của b khi chia cho 9
r là số dư của tích m.n khi chia cho 9, d là số dư của c khi chia cho 9
Điền vào các ô trống rồi so sánh r và d trong mỗi trường hợp sau :
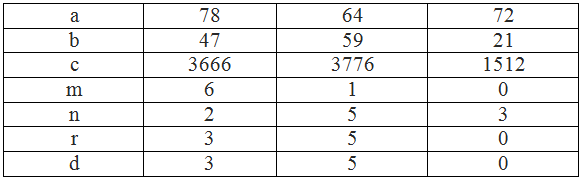
Trong phép nhân \(a.b=c\) gọi :
m là số dư của a khi chia cho 9, n là số dư của b khi chia cho 9
r là số dư của tích m.n khi chia cho 9, d là số dư của c khi chia cho 9
Điền vào các ô trống rồi so sánh r và d trong mỗi trường hợp sau :

Gọi m là số dư của a khi chia cho 9. Điền vào ô trống :
| a | 16 | 213 | 827 | 468 |
| m |
- Với a = 16 có tổng 1 + 6 = 7. Tổng này chia cho 9 dư 7 nên số này chia cho 9 dư 7. Do đó m = 7.
- Với a = 213 có tổng 2 + 1 + 3 = 6. Tổng này chia cho 9 dư 6 nên số này chia cho 9 dư 6. Do đó m = 6.
- Với a = 827 có tổng 8 + 2 + 7 = 17. Tổng này chia cho 9 dư 8 nên số này chia cho 9 dư 8. Do đó m = 8.
- Với a = 468 có tổng 4 + 6 + 8 = 18. Tổng này chia hết cho 9 (dư 0) nên số này chia hết cho 9. Do đó m = 0.
Dùng 3 trong bốn chữ 4, 5, 3, 0 hãy ghép thành các số tự nhiên có ba chữ số sao cho các số đó :
a) Chia hết cho 9
b) Chia hết cho 3 mà không chia hết cho 9
a) Số chia hết cho 9 thì tổng các chữ số của nó chia hết cho 9 \(\Rightarrow\) Các số cần tìm là: 450, 540, 405, 504.
b) Số chia hết cho 3 mà không chia hết cho 9 thì có tổng các chữ số của nó phải chia hết cho 3 mà không chia hết cho 9. Do đó các số cần tìm là:
543, 534, 453, 435, 345, 354.
Trả lời bởi QuìnMột số có tổng các chữ số chia cho 9 (cho 3) dư m thì số đó chia cho 9 (cho 3) cũng dư m
Ví dụ :
Số 1543 có tổng số các chữ số bằng : \(1+5+4+3=13\). Số 13 chia cho 9 dư 4, chia 3 dư 1. DO đó số 1543 chia 9 dư, chua 3 dư 1
Tìm số dư khi chia mỗi số sau cho 9, cho 3 : 1546; 1527; 2468; \(10^{11}\)
- Số 1546 có tổng 1 + 5 + 4 + 6 = 16. Tổng này chia cho 9 dư 7, chia cho 3 dư 1.
Do đó, số 1546 chia cho 9 dư 7, chia cho 3 dư 1.
- Số 1527 có tổng 1 + 5 + 2 + 7 = 15. Tổng này chia cho 9 dư 6, và chia hết cho 3.
Do đó, số 1527 chia cho 9 dư 6, và chia hết cho 3.
- Số 2468 có tổng 2 + 4 + 6 + 8 = 20. Tổng này chia cho 9 dư 2, chia cho 3 dư 2.
Do đó, số 2468 chia cho 9 dư 2, chia cho 3 dư 2.
- Số 1011 có tổng 1 + 0 + ... + 0 = 1. Tổng này chia cho 9 dư 1, chia cho 3 dư 1.
Do đó, số 1011 chia cho 9 dư 1, chia cho 3 dư 1.
Trả lời bởi Hai BinhViết số tự nhiên nhỏ nhất có năm chữ số sao cho số đó :
a) Chia hết cho 3
b) Chia hết cho 9
Điền chữ số vào dấu \(\circledast\) để :
a) \(\overline{5\circledast8}\) chia hết cho 3
b) \(\overline{6\circledast3}\) chia hết cho 9
c) \(\overline{43\circledast}\) chia hết cho cả 3 và 5
d) \(\overline{\circledast81\circledast}\) chia hết cho cả 2, 3, 5, 9 (Trong một số có nhiều dấu \(\circledast\), các dấu \(\circledast\) không nhất thiết thay bởi các chữ số giống nhau)
a)
\(\overline{5\circledast8}⋮3khi\left(5+\circledast+8\right)⋮3\Rightarrow\left(13+\circledast\right)⋮3\)
\(\Rightarrow\circledast\) = 2 hoặc \(\circledast\) = 5 hoặc \(\circledast\) = 8.
Vậy chữ số thay cho \(\circledast\) là 2 hoặc 5 hoặc 8.
b)
\(\overline{6\circledast3}⋮9khi\left(6+3+\circledast\right)⋮9\Rightarrow\left(9+\circledast\right)⋮9\)
\(\Rightarrow\circledast\) = 0 hoặc \(\circledast\) = 9.
Vậy chữ số thay \(\circledast\) là 0 hoặc 9
c)
\(\overline{43\circledast}⋮3khi\left(4+3+\circledast\right)⋮3\Rightarrow\circledast=2\text{hoặc}\circledast=5\text{hoặc}\circledast=8\left(1\right)\)
\(\overline{43\circledast}⋮5khi\circledast=0\text{hoặc}\circledast5\)
Vì \(\circledast\) phải thỏa mãn (1) và ( 2) nên \(\circledast\) = 5.
d)
Vì \(\overline{\circledast81\circledast}⋮5\) nên dấu \(\circledast\) ở hàng đơn vị phải bằng 0 hoặc 5
Mà \(\overline{\circledast81\circledast}⋮2\) nên dấu \(\circledast\) ở hàng đơn vị phải bằng 0 ( vì 5 là số lẻ ) . Thay vào ta được số : \(\overline{\circledast810}\)
Để \(\overline{\circledast810}⋮9\) thì \(\left(\circledast+8+1+0\right)⋮9=\left(\circledast+9\right)\Rightarrow\circledast=0\text{hoặc}\circledast=9\)
Mà \(\circledast\) lại là số ở hàng nghìn (là số đầu tiên) nên \(\circledast\) ≠ 0. Do đó \(\circledast\) = 9
Vậy ta được số 9810
Trả lời bởi Lam Ngo TungCho các số : \(3564;4352;6531;6570;1248\)
a) Viết tập hợp A các số chia hết cho 3 trong các số trên
b) Viết tập hợp B các số chia hết cho 9 trong các số trên
c) Dùng kí hiệu \(\subset\) để thể hiện quan hệ giữa hai tập hợp A và B
a) Vì 3564 có tổng các chữ số là 3 + 5 + 6 + 4 = 18, chia hết cho 3;
4352 có 4 + 3 + 5 + 2 = 14 không chia hết cho 3, không chia hết cho 9;
6531 có 6 + 5 + 3 + 1 = 15 chia hết cho 3;
6570 có 6 + 5 + 7 + 0 = 18 chia hết cho 9;
1248 có 1 + 2 + 4 + 8 = 15 chia hết cho 3.
Vậy A = {3564; 6531; 6570; 1248}
b) B = {3564; 6570.
c) B ⊂ A
Trong các số sau, số nào chia hết cho 3, số nào chia hết cho 9 ?
\(187;1347;2515;6534;93258\)
Tổng (hiệu) sau có chia hết cho 3 không, có chia hết cho 9 không ?
a) \(1251+5316\)
b) \(5436-1324\)
c) \(1.2.3.4.5.6+27\)
Bài giải:
HD: Có thể tính tổng (hiệu) rồi xét xem kết quả tìm được có chia hết cho 3, cho 9 không. Cũng có thể xét xem từng số hạng của tổng (hiệu) có chia hết cho 3, cho 9 không. Chẳng han: 1251 chia hết cho 3 và cho 9, 5316 chỉ chia hết cho 3 mà không chia hết cho 9. Do đó tổng 1251 + 5316 chia hết cho 3 mà không chia hết cho 9.
Đáp số:
a) 1251 + 5316 chia hết cho 3 mà không chia hết cho 9.
b) 5436 - 1324 không chia hết cho 3, không chia hết cho 9.
c) Vì 1 . 2 . 3 . 4 . 5 . 6 = 1 . 2 . 3 . 4 . 5 . 3 . 2 = 9 . 1 . 2 . 4 . 5 . 2 chia hết cho 9 và 27 cũng chia hết cho 9 nên 1 . 2 . 3 . 4 . 5 . 6 + 27 chia hết cho 9. Do đó cũng chia hết cho 3.
Điền dấu "X" vào ô thích hợp trong các câu sau :

Trả lời bởi Phan Thùy Linh