a) Sử dụng máy tính cầm tay, hoàn thành bảng sau vào vở (làm tròn kết quả đến chữ số thập phân thứ năm).
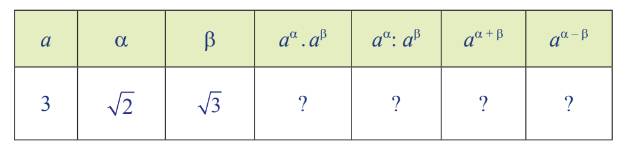
b) Từ kết quả quả ở câu a, có dự đoán gì về tính chất của phép tính luỹ thừa với số mũ thực?
a) Sử dụng máy tính cầm tay, hoàn thành bảng sau vào vở (làm tròn kết quả đến chữ số thập phân thứ năm).

b) Từ kết quả quả ở câu a, có dự đoán gì về tính chất của phép tính luỹ thừa với số mũ thực?
Viết các biểu thức sau dưới dạng một luỹ thừa \(\left( {a > 0} \right)\):
a) \({a^{\frac{3}{5}}}.{a^{\frac{1}{2}}}:{a^{ - \frac{2}{5}}}\);
b) \(\sqrt {{a^{\frac{1}{2}}}\sqrt {{a^{\frac{1}{2}}}\sqrt a } } \).
\(a,a^{\dfrac{3}{5}}\cdot a^{\dfrac{1}{2}}:a^{-\dfrac{2}{5}}=a^{\dfrac{3}{5}+\dfrac{1}{2}-\left(-\dfrac{2}{5}\right)}=a^{\dfrac{3}{2}}\\ b,\sqrt{a^{\dfrac{1}{2}}\sqrt{a^{\dfrac{1}{2}}\sqrt{a}}}\\ =\sqrt{a^{\dfrac{1}{2}}\sqrt{a^{\dfrac{1}{2}}\cdot a^{\dfrac{1}{2}}}}\\ =\sqrt{a^{\dfrac{1}{2}}\sqrt{a}}\\ =\sqrt{a^{\dfrac{1}{2}}\cdot a^{\dfrac{1}{2}}}\\ =\sqrt{a}\)
Trả lời bởi Hà Quang MinhRút gọn biểu thức: \({\left( {{x^{\sqrt 2 }}y} \right)^{\sqrt 2 }}\left( {9{y^{ - \sqrt 2 }}} \right)\) (với \(x,y > 0\)).
$\left(x^{\sqrt{2}}y\right)^{\sqrt{2}} = x^{\sqrt{2} \cdot \sqrt{2}}y^{\sqrt{2}} = x^2y^{\sqrt{2}}$
$x^2y^{\sqrt{2}} \cdot 9y^{-\sqrt{2}} = 9x^2y^{\sqrt{2}}y^{-\sqrt{2}} = 9x^2$
Trả lời bởi HaNaTính giá trị các biểu thức sau:
a) \({\left( {\frac{3}{4}} \right)^{ - 2}}{.3^2}{.12^0}\);
b) \({\left( {\frac{1}{{12}}} \right)^{ - 1}}.{\left( {\frac{2}{3}} \right)^{ - 2}}\);
c) \({\left( {{2^{ - 2}}{{.5}^2}} \right)^{ - 2}}:\left( {{{5.5}^{ - 5}}} \right)\).
a) \(\left(\dfrac{3}{4}\right)^{-2}\cdot3^2\cdot12^0=16\)
b) \(\left(\dfrac{1}{12}\right)^{-1}\cdot\left(\dfrac{2}{3}\right)^{-2}=27\)
c) \(\left(2^{-2}\cdot5^2\right)^{-2}:\left(5\cdot5^{-5}\right)=16\)
Trả lời bởi HT.Phong (9A5)Viết các biểu thức sau dưới dạng một luỹ thừa \(\left( {a > 0} \right)\):
a) \(3.\sqrt 3 .\sqrt[4]{3}.\sqrt[8]{3}\);
b) \(\sqrt {a\sqrt {a\sqrt a } } \);
c) \(\frac{{\sqrt a .\sqrt[3]{a}.\sqrt[4]{a}}}{{{{\left( {\sqrt[5]{a}} \right)}^3}.{a^{\frac{2}{5}}}}}\).
a: \(=3\cdot3^{\dfrac{1}{2}}\cdot3^{\dfrac{1}{.4}}\cdot3^{\dfrac{1}{8}}=3^{1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}}=3^{\dfrac{15}{16}}\)
b: \(=\sqrt{a\cdot\sqrt{a\cdot a^{\dfrac{1}{2}}}}\)
\(=\sqrt{a\cdot\sqrt{a^{\dfrac{3}{2}}}}=\sqrt{a\cdot a^{\dfrac{3}{4}}}=\sqrt{a^{\dfrac{7}{4}}}=a^{\dfrac{7}{4}\cdot\dfrac{1.}{2}}=a^{\dfrac{7}{8}}\)
c: \(=\dfrac{a^{\dfrac{1}{2}}\cdot a^{\dfrac{1}{3}}\cdot a^{\dfrac{1}{4}}}{\left(a^{\dfrac{1}{5}}\right)^3\cdot a^{\dfrac{2}{5}}}=\dfrac{a^{\dfrac{13}{12}}}{a}=a^{\dfrac{1}{12}}\)
Trả lời bởi Nguyễn Lê Phước ThịnhRút gọn các biểu thức sau \(\left( {a > 0,b > 0} \right)\):
a) \({a^{\frac{1}{3}}}{a^{\frac{1}{2}}}{a^{\frac{7}{6}}}\);
b) \({a^{\frac{2}{3}}}{a^{\frac{1}{4}}}:{a^{\frac{1}{6}}}\);
c) \(\left( {\frac{3}{2}{a^{ - \frac{3}{2}}}{b^{ - \frac{1}{2}}}} \right)\left( { - \frac{1}{3}{a^{\frac{1}{2}}}{b^{\frac{3}{2}}}} \right)\).
a) \(a^{\dfrac{1}{3}}\cdot a^{\dfrac{1}{2}}\cdot a^{\dfrac{7}{6}}=a^{\dfrac{1}{3}+\dfrac{1}{2}+\dfrac{7}{6}}=a^2\)
b) \(a^{\dfrac{2}{3}}\cdot a^{\dfrac{1}{4}}:a^{\dfrac{1}{6}}=a^{\dfrac{2}{3}+\dfrac{1}{4}-\dfrac{1}{6}}=a^{\dfrac{3}{4}}\)
c) \(\left(\dfrac{3}{2}a^{-\dfrac{3}{2}}\cdot b^{-\dfrac{1}{2}}\right)\left(-\dfrac{1}{3}a^{\dfrac{1}{2}}b^{\dfrac{2}{3}}\right)=\left(\dfrac{3}{2}\cdot-\dfrac{1}{3}\right)\left(a^{-\dfrac{3}{2}}\cdot a^{\dfrac{1}{2}}\right)\left(b^{-\dfrac{1}{2}}\cdot b^{\dfrac{2}{3}}\right)\)
\(=-\dfrac{1}{2}a^{-1}b^{-\dfrac{1}{3}}\)
Trả lời bởi HT.Phong (9A5)Với một chỉ vàng, giả sử người thợ lành nghề có thể dát mỏng thành lá vàng rộng \(1\,{m^2}\) và dày khoảng \(1,{94.10^{ - 7}}\,m\). Đồng xu 5.000 đồng dày \(2,{2.10^{ - 3}}\,m\). Cần chồng bao nhiêu lá vàng như trên để có độ dày bằng đồng xu loại 5000 đồng? Làm tròn kết quả đến chữ số hàng trăm.
Số lá vàng cần trồng là;
\(\dfrac{2.2\cdot10^{-3}}{1.94\cdot10^{-7}}\simeq11300\left(lá\right)\)
Trả lời bởi Nguyễn Lê Phước ThịnhTại một xí nghiệp, công thức \(P\left( t \right) = 500.{\left( {\frac{1}{2}} \right)^{\frac{t}{3}}}\) được dùng để tính giá trị còn lại (tính theo triệu đồng) của một chiếc máy sau thời gian \(t\) (tính theo năm) kể từ khi đưa vào sử dụng.
a) Tính giá trị còn lại của máy sau 2 năm; sau 2 năm 3 tháng.
b) Sau 1 năm đưa vào sử dụng, giá trị còn lại của máy bằng bao nhiêu phần trăm so với ban đầu?
a)
$P(2) = 500 \left(\frac{1}{2}\right)^{\frac{2}{3}}$
$P(2.25) = 500 \left(\frac{1}{2}\right)^{\frac{2.25}{3}}$
b)
$P(1) = 500 \left(\frac{1}{2}\right)^{\frac{1}{3}}$
Phần trăm giá trị còn lại so với ban đầu sau 1 năm là: `\frac{P(1)}{500} \times 100%=79%`
Trả lời bởi HaNaBiết rằng \({10^\alpha } = 2;{10^\beta } = 5\).
Tính \({10^{\alpha + \beta }};{10^{\alpha - \beta }};{10^{2\alpha }};{10^{ - 2\alpha }};{1000^\beta };0,{01^{2\alpha }}\).
Ta có:
\(10^{\alpha}=2\Rightarrow\alpha=log_{10}2\)
\(10^{\beta}=5\Rightarrow\beta=log_{10}5\)
Kết quả:
\(10^{\alpha+\beta}=10^{log_{10}2+log_{10}5}=10\)
\(10^{2\cdot log_{10}2}=4\)
\(1000^{log_{10}5}=125\)
\(0,01^{2\cdot log_{10}2}=\dfrac{1}{16}\)
Trả lời bởi HT.Phong (9A5)Biết rằng \({4^\alpha } = \frac{1}{5}\). Tính giá trị các biểu thức sau:
a) \({16^\alpha } + {16^{ - \alpha }}\);
b) \({\left( {{2^\alpha } + {2^{ - \alpha }}} \right)^2}\).
a)
$16^{\alpha }+16^{-\alpha } = (4^2)^{\alpha }+(4^2)^{-\alpha } = 4^{2\alpha }+4^{-2\alpha }$
$4^{2\alpha }+4^{-2\alpha } = 4^{2\log_4{\frac{1}{5}}}+4^{-2\log_4{\frac{1}{5}}} = \left(\frac{1}{5}\right)^2+\left(\frac{1}{5}\right)^{-2} = \frac{1}{25}+25 = \frac{26}{25}$
Trả lời bởi HaNa
a)
\(\sqrt{2}\)
b) Nhận xét:
\(a^m\cdot a^n=a^{m+n};a^m:a^n=a^{m-n}\)
Trả lời bởi HT.Phong (9A5)