Học tại trường
Chưa có thông tin
Đến từ
Đà Nẵng , Chưa có thông tin
Số lượng câu hỏi
0
Số lượng câu trả lời
820
Điểm GP
465
Điểm SP
966
Người theo dõi (25)
Đang theo dõi (2)
AT
Câu trả lời:
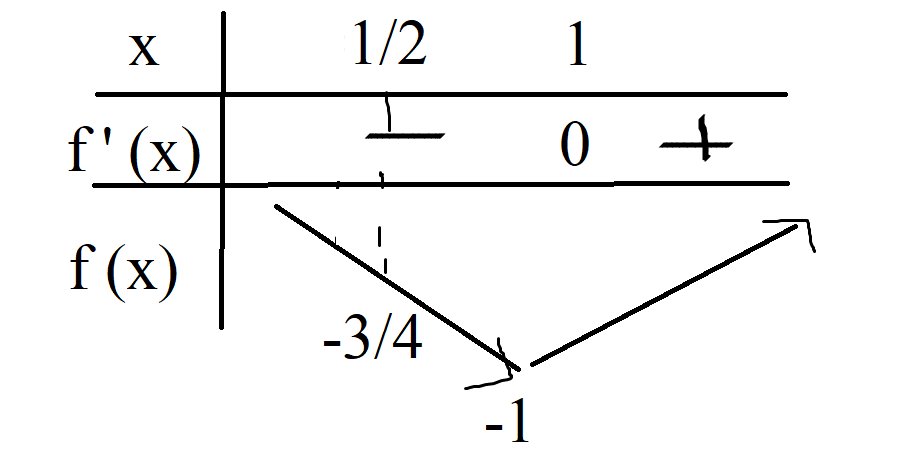
bbt: 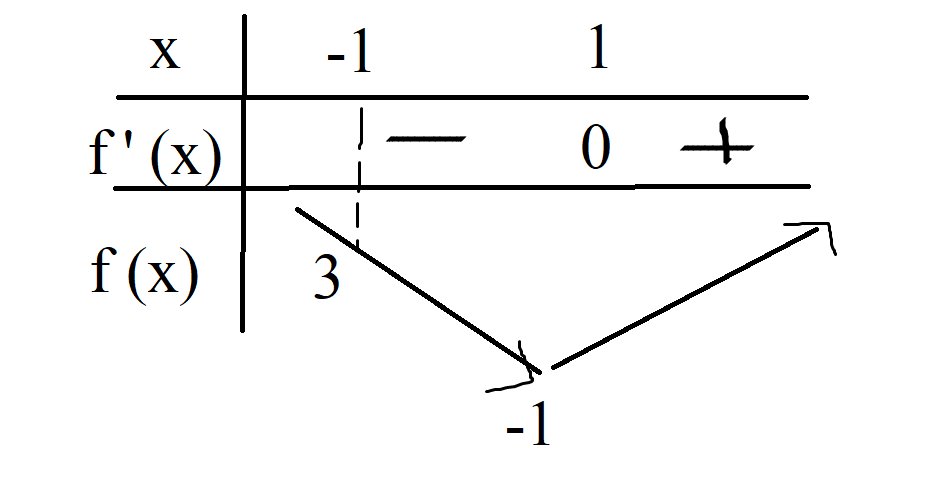
\(\Rightarrow1-m\le-1\Rightarrow m\ge2\)
AT
Câu trả lời:
bbt: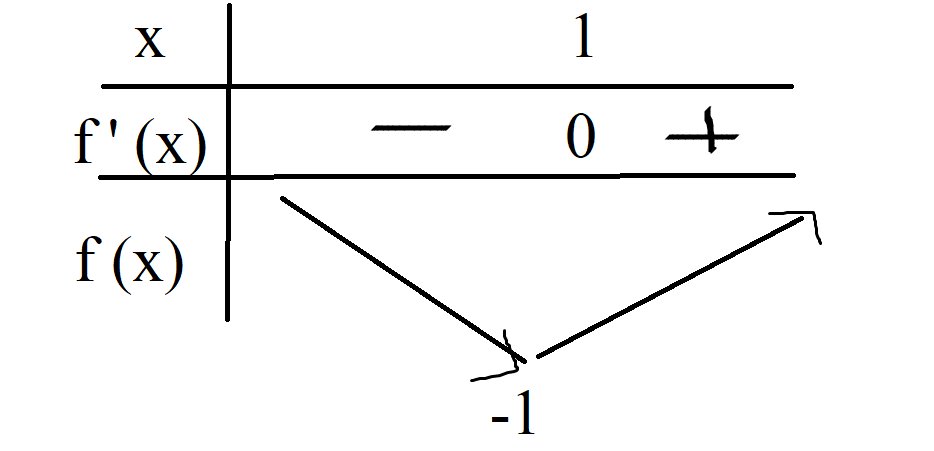
AT
Câu trả lời:
thế điểm A(-4;1) vào đó bạn nên 1=2(-4)+b